REMA-3 : Régression linéaire et logistique avec R
On a précédemment vu comment on pouvait organiser et visualiser nos données.
Maintenant, plus le choix, on doit se retrousser les manches et les analyser
C’est un moyen intéressant de comprendre votre BD avant même de faire des statistiques.
Comme pour tout le reste, ce travail est un travail en progression, donc n’hésitez pas si il y a des coquilles ou problèmes à me les signaler pour que je les corrige s.buczinski@umontreal.ca
AVERTISSEMENT: CE TUTORIEL N’EST EN AUCUN CAS UN COURS DE STATISTIQUES OU D’ÉPIDÉMIOLOGIE. IL SE VEUT UNE AIDE AUX ÉTUDIANTS OU PERSONNES PLUS AXÉES SUR LA CLINIQUE AFIN DE NOTAMMENT COMPRENDRE ET ANALYSER UNE BASE DE DONNÉES PAR SOI MÊME. IL EST TOUJOURS RECOMMANDÉ DE CONSULTER UNE PERSONNE AYANT DE BONNES BASES EN ÉPIDÉMIOLOGIE ET/OU STATISTIQUES AFIN DE S’ASSURER DE LA PERTINENCE DE LA STRATÉGIE ADOPTÉE…
ET RAPPELEZ VOUS BIEN:
“Science sans conscience n’est que ruine de l’âme…” (Tiré de Rabelais (Pantagruel, 1532))
Vous pouvez vous référer à tout moment à cet exposé qui aborde de façon beaucoup plus savante que moi les sujets tournant autour de la régression => Cours récent sur le sujet de la régression de Frank Harrell. Je vous renvoie aussi aux cours d’épidémiologie / statistiques.
Autre chose à garder toujours en tête : Les limites des valeurs de P. Là aussi je ne m’y étendrais pas mais c’est TRÈS important…
1 Régression linéaire
1.1 Principes de base
On veut montrer une relation linéaire car c’est le plus simple mais ce n’est pas nécessairement la meilleure façon tout le temps de démontrer une relation…

Comment choisir la meilleure relation??
Un résumé simple: la régression linéaire a pour but (comme vous le savez) de trouver une relation linéaire donc en forme de droite entre une variable dépendante \(Y\) et des variables indépendantes ou covariables ( mes \(x\)’s). On commence notamment avec la régression linéaire (qui consiste à trouver les coefficients et l’intercept de la droite représentant le mieux le nuage de points…) car elle est le point de départ qui permet à notre esprit de bien se représenter ce que l’on veut mettre en évidence.
Donc si on met cela sous forme plus mathématique on obtient:
\[Y= b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n} + \epsilon\ \]
soit encore plus compact:
\[Y= \sum_{i=0}^{n} b_{i}x_{i} + \epsilon\ \] ou en écriture matricielle:
\[Y=bX\] Donc en gros on veut trouver les coefficients de chaque variable représentant leur effet sur Y en contrôlant pour les autres facteurs présents. Notez le \(b_{0}\) qui est l’intercept lorsque tous les \(x_{i}\) sont nuls. On parle toujours ou quasiment de la régression linéaire sachant que ce que l’on veut dire est que notre Y évolue linéairement face à une augmentation de nos \(x_{i}\) ou de leur transformation (par exemple \(Y\) peut ne pas évoluer linéairement avec notre \(x\) brut mais la relation peut devenir linéaire si on transforme \(x\) avec par exemple \(x_{transf}=log(x)\) ou bIen d’autres transformations…).
Enfin même si on aime les lignes droites il faut aussi se dire que la régression linéaire n’est pas nécessairement la relation la plus judicieuse ou mathématiquement valide selon les cas. D’où l’importance de s’assurer que notre compréhension du problème vs son analyse sont adéquats.
C’est cependant ce qu’il y a de plus simple pour commencer et pour comprendre.
La régression linéaire ne se prête qu`à l’analyse des \(Y\) qui sont des variables quantitatives continues et a différentes conditions d’applications.
RAPPELEZ VOUS: MÊME SI VOUS AVEZ UNE RÉPONSE DE VOTRE LOGICIEL POUR UN MODELE PARTICULIER, IL EST TOUJOURS FONDAMENTAL DE S’ASSURER QUE VOTRE MODÈLE EST BIEN APPLICABLE ET/OU VALIDE.
JE FERAI L’ANALOGIE SUIVANTE: MÊME SI TOUT LE MONDE PEUT POTENTIELLEMENT SUIVRE UN TUTORIEL POUR RÉPARER UNE PANNE ÉLECTRIQUE, TOUT LE MONDE NE PEUT PAS GARANTIR QUE LES CONDITIONS DANS LESQUELLES SONT FAITES LA RÉPARATION SONT SÉCURITAIRES (IE QUE VOTRE MAISON NE BRULERA PAS SUITE À UN COURT-CIRCUIT). C’EST POUR CELA QUE JE ME FIE PLUS À MON ÉLECTRICIEN CERTIFIÉ QU’À MOI MÊME.
C’EST LA MÊME CHOSE AVEC N’IMPORTE QUEL LOGICIEL. IL EST DONC FONDAMENTAL DE VOUS ASSURER DE LA VALIDITÉ DE VOTRE MODÈLE LORS DE DIFFÉRENTES ÉTAPES DE CONSTRUCTION ET DE VALIDATION DE CE DERNIER.
1.2 Relation avec une seule variable (analyse univariée)
Préambule : Chargement des packages nécessaires au tutoriel
library(tidyverse)#suite du tidyverse incluant ggplot2 notamment
library(readxl)
library(ggpubr) #différentes fonctionnalités incluant les tests de normalité
library(funModeling) #pour décrir et utiliser des fonctionnalités en univarié
library(sjPlot)# pour imager les résultats de votre modèle de régression
library(broom) # pour visualiser les erreurs entre prédictions et observationsNB: je ne parle pas du paquet lme4 ou son équivalent Bayésien brms que l’on peut utiliser avec ses différentes fonctions pour la plupart des modèles avec un effet aléatoire (modèles mixtes)
Dans cette portion nous allons définir notre variable d’intérêt qui est notre variable dépendante ou \(Y\). Nous voulons trouver une relation linéaire décrivant cette variable en fonction des autres variables dites indépendantes (nos \(x\)’s).
Comme tout modèle mathématique il y a des assomptions à vérifier et qui sont fondamentales (surtout si on veut être sûr que notre interprétation est adéquate):
- la relation est linéaire entre le \(Y\) et son/ses \(x\)’s
- les variables continues sont normales (à peu près)
- il n’y a pas de colinéarité entre mes \(x\)’s
- il n’y a pas de corrélation entre mes \(y\) (par exemple je ne pourrais pas utiliser les données des mêmes animaux à différents moments sans tenir compte que ces données viennent des mêmes individus et sont donc corrélés)
- il y a homoscédasticité : donc la variance de mon modèle ne dépend pas des valeurs de \(y\) ou de \(x\). En des termes plus simples on veut que l’erreur de notre modèle (\(\epsilon\) ) est distribuée normalement (de moyenne 0) autour de notre droite de régression….
NB: et cela en général la plupart des logiciels dans lesquels vous allez tenter de faire une analyse ne vont pas faire toutes ces étapes systématiquement et de façon informative pour vous => donc cela va nécessiter d’aller vous-même vous en assurer
1.2.1 Évaluation de la variable dépendante continue
Tout d’abord nous devons trouver une base de données qui nous permette d’illustrer le tout. Encore une fois je vais utiliser une base de données facilement accessible et tirée du site du livre de Ian Dohoo. Ici j’ai utlilisé une BD sous format excel qui évalue la qualité de la viande en fonction de différents critères échographiques et morphologiques. Je nommerai cette BD beef par la suite.
#importer la base de données
beef <- read_excel("beef_ultra.xlsx")
head(beef, n=10)## # A tibble: 10 x 12
## farm id grade breed sex bckgrnd implant backfat ribeye imfat days
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 43 2 9 0 1 0 5.39 10.3 1.85 99
## 2 1 46 2 11 0 1 0 2.16 9.47 1.85 315
## 3 1 56 2 8 0 1 0 2.03 8.66 1.85 99
## 4 3 162 2 7 0 1 0 3.14 8.99 1.85 158
## 5 3 187 1 15 1 1 0 3.14 10.5 1.85 195
## 6 3 221 3 9 1 1 0 3.37 13.3 1.85 164
## 7 3 227 2 8 0 1 0 2.29 5.99 1.85 175
## 8 3 236 3 8 0 1 0 3.37 8.71 1.85 154
## 9 4 266 2 8 1 0 1 3.14 8.97 1.85 217
## 10 5 359 2 10 1 0 0 2.03 10.5 1.85 271
## # ... with 1 more variable: carc_wt <dbl>Je regarde plus spécifquement la structure de cette base de données:
str(beef)## tibble [487 x 12] (S3: tbl_df/tbl/data.frame)
## $ farm : num [1:487] 1 1 1 3 3 3 3 3 4 5 ...
## $ id : num [1:487] 43 46 56 162 187 221 227 236 266 359 ...
## $ grade : num [1:487] 2 2 2 2 1 3 2 3 2 2 ...
## $ breed : num [1:487] 9 11 8 7 15 9 8 8 8 10 ...
## $ sex : num [1:487] 0 0 0 0 1 1 0 0 1 1 ...
## $ bckgrnd: num [1:487] 1 1 1 1 1 1 1 1 0 0 ...
## $ implant: num [1:487] 0 0 0 0 0 0 0 0 1 0 ...
## $ backfat: num [1:487] 5.39 2.16 2.03 3.14 3.14 ...
## $ ribeye : num [1:487] 10.29 9.47 8.66 8.99 10.55 ...
## $ imfat : num [1:487] 1.85 1.85 1.85 1.85 1.85 ...
## $ days : num [1:487] 99 315 99 158 195 164 175 154 217 271 ...
## $ carc_wt: num [1:487] 284 358 293 291 395 ...summary(beef)## farm id grade breed
## Min. :1.000 Min. : 1.0 Min. :1.000 Min. : 1.000
## 1st Qu.:3.000 1st Qu.:123.5 1st Qu.:1.000 1st Qu.: 5.000
## Median :3.000 Median :249.0 Median :2.000 Median : 8.000
## Mean :3.764 Mean :248.7 Mean :1.758 Mean : 8.006
## 3rd Qu.:5.000 3rd Qu.:373.5 3rd Qu.:2.000 3rd Qu.:11.000
## Max. :8.000 Max. :497.0 Max. :3.000 Max. :15.000
## sex bckgrnd implant backfat
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.900
## 1st Qu.:0.0000 1st Qu.:1.0000 1st Qu.:0.0000 1st Qu.:2.250
## Median :1.0000 Median :1.0000 Median :0.0000 Median :2.725
## Mean :0.6448 Mean :0.7536 Mean :0.2649 Mean :3.081
## 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:3.590
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :8.755
## ribeye imfat days carc_wt
## Min. : 4.620 Min. :1.850 Min. : 15.0 Min. :209.1
## 1st Qu.: 7.640 1st Qu.:3.510 1st Qu.:166.0 1st Qu.:299.8
## Median : 8.535 Median :3.980 Median :217.0 Median :327.3
## Mean : 8.843 Mean :4.116 Mean :213.4 Mean :330.6
## 3rd Qu.: 9.717 3rd Qu.:4.657 3rd Qu.:267.0 3rd Qu.:360.5
## Max. :17.235 Max. :8.360 Max. :614.0 Max. :474.512 variables, 487 observations…
Je peux aussi avoir quelque chose de plus graphique et visuel avec le paquet summarytools comme présenté dans REMA-1.
library(summarytools) #permet d'avoir des outputs plus "friendly users"
#n'oubliez pas de le charger une première fois avec install.package()
print(dfSummary(beef, valid.col = FALSE, graph.magnif = 0.75),
max.tbl.height = 300, method = "render")Data Frame Summary
beef
Dimensions: 487 x 12Duplicates: 0
| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Missing | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | farm [numeric] | Mean (sd) : 3.8 (1.9) min < med < max: 1 < 3 < 8 IQR (CV) : 2 (0.5) |
|
0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | id [numeric] | Mean (sd) : 248.7 (144.1) min < med < max: 1 < 249 < 497 IQR (CV) : 250 (0.6) | 487 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | grade [numeric] | Mean (sd) : 1.8 (0.6) min < med < max: 1 < 2 < 3 IQR (CV) : 1 (0.3) |
|
0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | breed [numeric] | Mean (sd) : 8 (3.9) min < med < max: 1 < 8 < 15 IQR (CV) : 6 (0.5) | 15 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | sex [numeric] | Min : 0 Mean : 0.6 Max : 1 |
|
0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | bckgrnd [numeric] | Min : 0 Mean : 0.8 Max : 1 |
|
0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | implant [numeric] | Min : 0 Mean : 0.3 Max : 1 |
|
0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | backfat [numeric] | Mean (sd) : 3.1 (1.2) min < med < max: 0.9 < 2.7 < 8.8 IQR (CV) : 1.3 (0.4) | 97 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | ribeye [numeric] | Mean (sd) : 8.8 (1.9) min < med < max: 4.6 < 8.5 < 17.2 IQR (CV) : 2.1 (0.2) | 391 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | imfat [numeric] | Mean (sd) : 4.1 (1) min < med < max: 1.9 < 4 < 8.4 IQR (CV) : 1.1 (0.2) | 332 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | days [numeric] | Mean (sd) : 213.4 (83.6) min < med < max: 15 < 217 < 614 IQR (CV) : 101 (0.4) | 137 distinct values | 0 (0%) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | carc_wt [numeric] | Mean (sd) : 330.6 (43.9) min < med < max: 209.1 < 327.3 < 474.5 IQR (CV) : 60.7 (0.1) | 251 distinct values | 0 (0%) |
Generated by summarytools 0.9.6 (R version 4.0.2)
2020-07-01
Donc on voit que cette base de données évalue différentes caractéristiques de la carcasse (grade, backfat, ribeye, imfat, carcass_weight) avec d’autres paramètres tels que le sexe, la race, le fait que l’animal ait été implanté ou pas. On voit aussi que cette base de données est parfaite car il n’y a aucune données manquantes (c’est plutot rare comme trouvaille donc je tiens à le souligner!!!) => par défaut toutes ces variables ont été reconnues comme variables numériques.
On veut répondre à la question : quels sont les facteurs associés au poids carcasse carc_wt (notre \(Y\))
Plus spécifiquement, notre variable dépendante a la distribution suivante (voir REMA-2 pour un rappel sur le fonctionnement de ggplot2):
ggplot(beef, aes(x=carc_wt)) + geom_histogram(fill="darkblue") + theme_classic()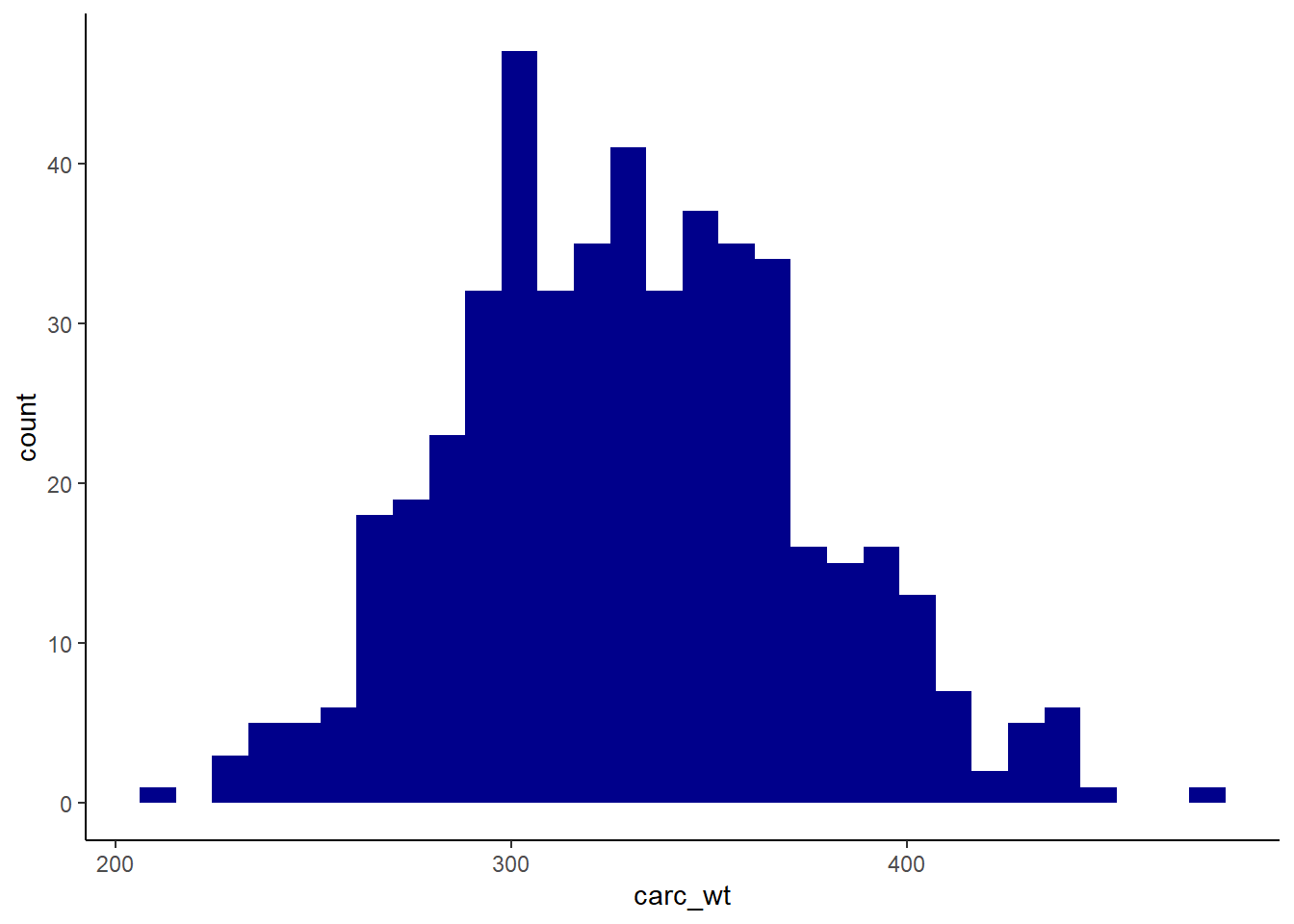
Bon, globalement on voit que notre variable est relativement proche de la distribution normale. Je vais le tester spécifiquement (voir lien suivant)
#ici j'utilise une fonction de ggpubr pour voir le qqplot (distribution selon les quantiles)
ggqqplot(beef$carc_wt)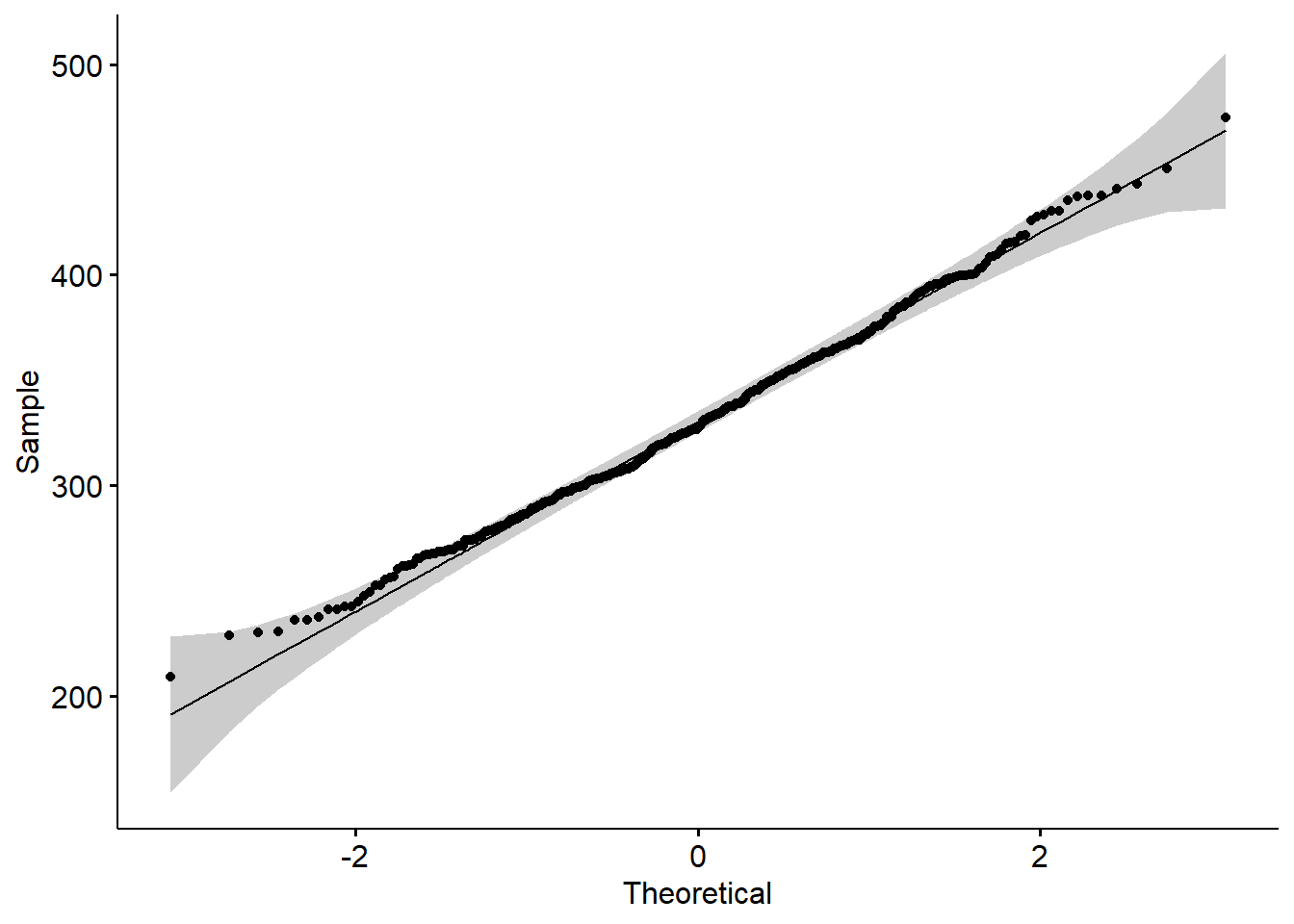
Grosso modo on voit que visuellement ce n’est vraiment pas si mal (nos points sont très proches de la ligne de référence de nos quantiles d’une loi normale) => Moi cela me suffit pour me dire que ma variable dépendante est distribuée normalement.
Cependant je peux bien sur le tester d’un point de vue statistique (par exemple par la méthode de Shapiro-Wilk ). J’aime bien la méthode de Shapiro-Wilk car elle est notamment plus robuste à des faibles tailles d’échantillon (ce n’est pas le cas ici) versus Kolmogorov-Smirnov par exemple…
Je l’appelle simplement par la commande shapiro.test().
shapiro.test(beef$carc_wt)##
## Shapiro-Wilk normality test
##
## data: beef$carc_wt
## W = 0.99539, p-value = 0.1598Ici je vois que la valeur de P est >.05 donc je ne peux pas rejeter l’hypothèse nulle (H0= ma variable est distribuée normalement) => je suis donc conforté sur la véracité de mon évaluation visuelle ….
1.2.2 Covariable continue
La base de données contient des variables qui sont continues et d’autres catégoriques ordonnées ou pas.
Évaluons dans un premier temps le lien entre le poids et le nombre de jours d’engraissement (days)
ggplot(beef, aes(x=days, y=carc_wt)) + geom_point() +theme_bw()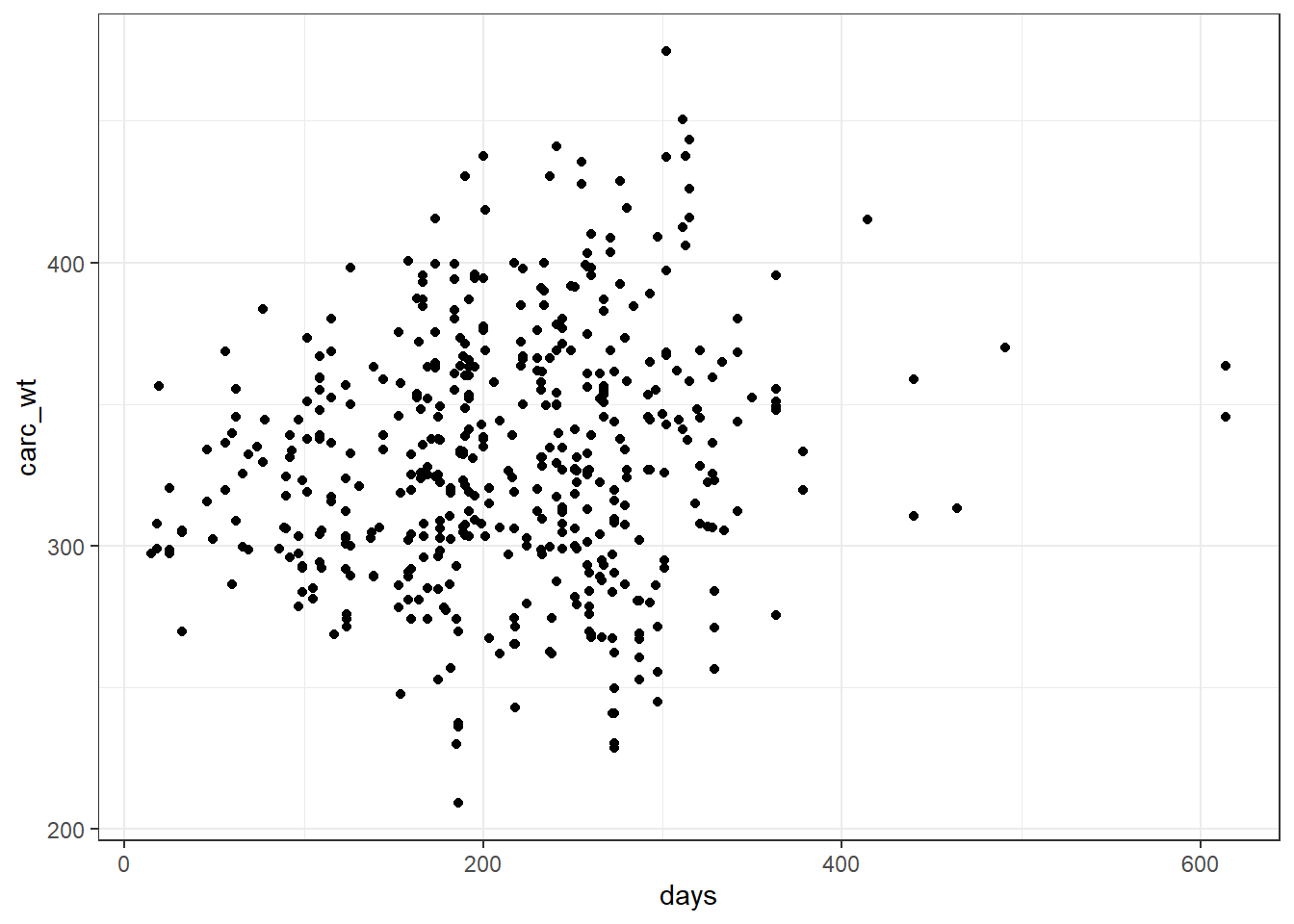
Donc visuellement pas grand chose d’évident si ce n’est un possible effet d’augmentation du poids en fonction du nombre de jours d’engraissement…
Ce que l’on remarque aussi est la dispersion des points sur l’axe des \(y\). Donc même si je trouve une relation linéaire, la portion de la variabilité de mon \(y\) prédite par la droite par la variation de mon \(x\) (days) sera assez limitée… (on y reviendra par le calcul des coefficients de corrélation et détermination \(R\) et \(R^2\))
ggplot(beef, aes(x=days)) + geom_histogram(fill="darkblue") +theme_classic()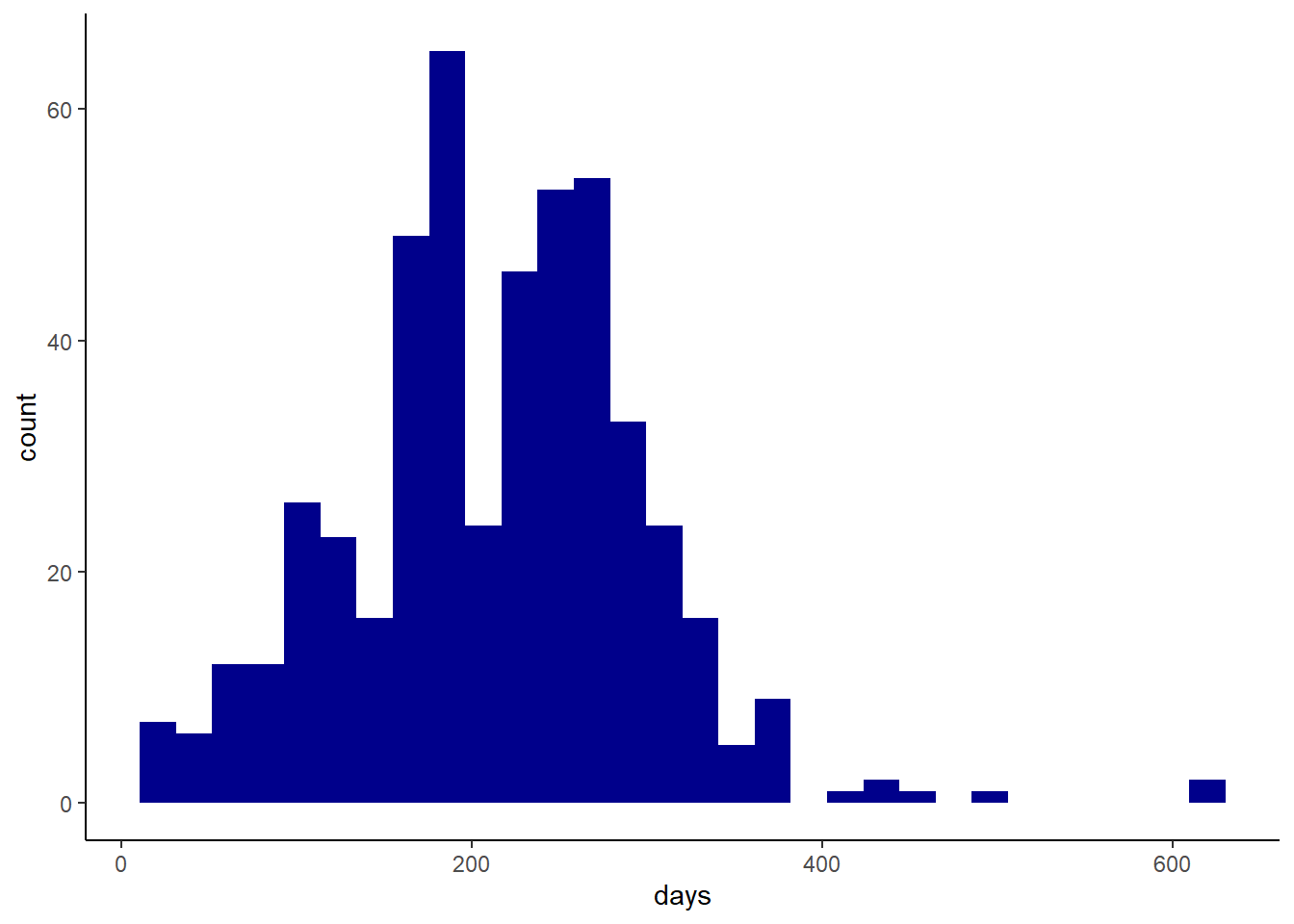
#je regarde aussi ma distribution
ggqqplot(beef$days)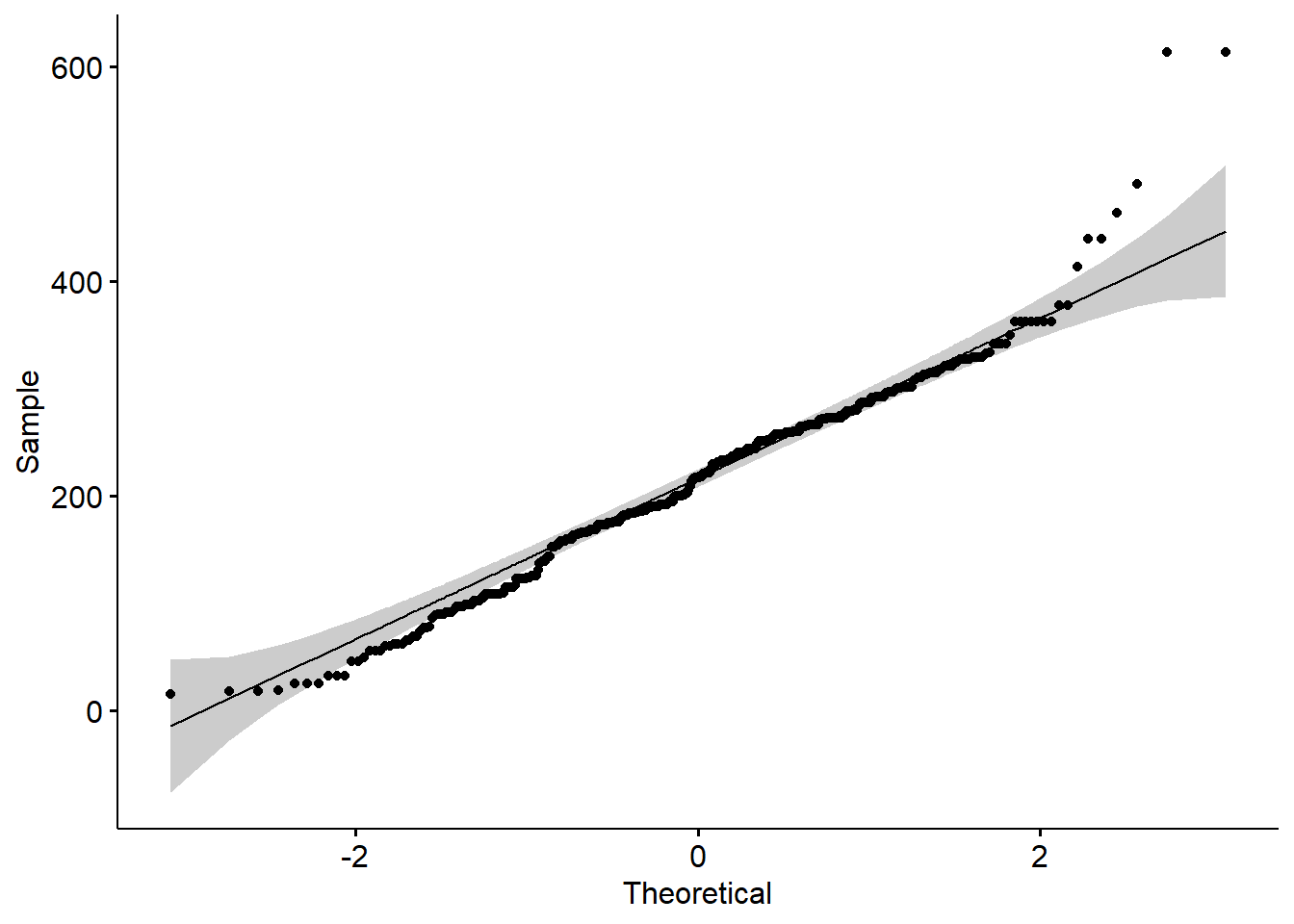
shapiro.test(beef$days)##
## Shapiro-Wilk normality test
##
## data: beef$days
## W = 0.9744, p-value = 1.585e-07Ici je vois que mes données sont non-normalement distribuées pour le nombre de jours. Je pourrais vivre avec cela et regarder juste à la fin si mes résidus du modèle sont distribués normalement ou pas. Ou je peux aussi d’emblée essayer de le changer…. Dans un premier temps on va vivre avec (il y a des choses plus stressantes dans la vie…). Encore une fois je vous montre les principes et ne veux pas m’étendre sur des débats mathématiques.
Mon but est tout d’abord de déterminer quel est l’effet de l’augmentation d’une unité de \(x\) sur mon \(Y\) donc l’effet d’un jour de plus en engraissement sur mon poids…

Interprétation des coefficients de régression linéaire
Je vais simplement utiliser la fonction lm() qui est une fonction de base dans R.
Notez que très rapidement je stocke le résultat dans un objet m_1 qui me servira ensuite pour tout…
m_1 <- lm(carc_wt~days, data=beef) # je spécifie Y (carc_2) qui dépend (~) de X (days) dans ma BD (argument data=beef)
# et c'est tout!
m_1##
## Call:
## lm(formula = carc_wt ~ days, data = beef)
##
## Coefficients:
## (Intercept) days
## 314.85211 0.07369On a d’emblée une réponse à notre question l’effet de chaque jour supplémentaire est de 73.7g.
Maintenant il faut en savoir plus avec la fonction summary et notamment si cet effet est différent de 0 ou pas d’un point de vue statistique…
summary(m_1)##
## Call:
## lm(formula = carc_wt ~ days, data = beef)
##
## Residuals:
## Min 1Q Median 3Q Max
## -119.468 -29.530 -1.643 29.143 137.438
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 314.85211 5.40923 58.206 <2e-16 ***
## days 0.07369 0.02360 3.122 0.0019 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 43.52 on 485 degrees of freedom
## Multiple R-squared: 0.0197, Adjusted R-squared: 0.01768
## F-statistic: 9.749 on 1 and 485 DF, p-value: 0.001902Ici tout est résumé rapidement dans ce panneau: Nous avons des paramètres de distribution des résidus… (à priori la médiane est proche de 0 et la distribution (en tout cas ses bornes) sont proches d’être symétriques…)
L’intercept et le coefficient jours sont significativement différents de 0. Pour notre covariable days la valeur de P est de .0019.
On peut aussi noter que le coefficient de détermination du modèle (\(R^2\) est de 0.02). Donc même si c’est significatif, le nombre de jours n’explique qu’une très faible partie du poids… (ce qui se résumait bien à partir du geom_point() avec une forte dispersion des points…).
1.2.2.1 Adéquation du modèle
Très facilement je peux regarder cela dans les diagnostiques de mon modèle m_1 par la fonction plot().
NB: Veuillez notez que la fontion plot() est assez générale dans R. Par défaut lorsque vous utilisez différentes fonctions sur R et que vous avez un objet, plot(objet) vous fourni les illustrations de base associées à la fonction (par défaut)..
par(mfrow = c(2, 2)) #je mets les graphs sur le même panneau
plot(m_1)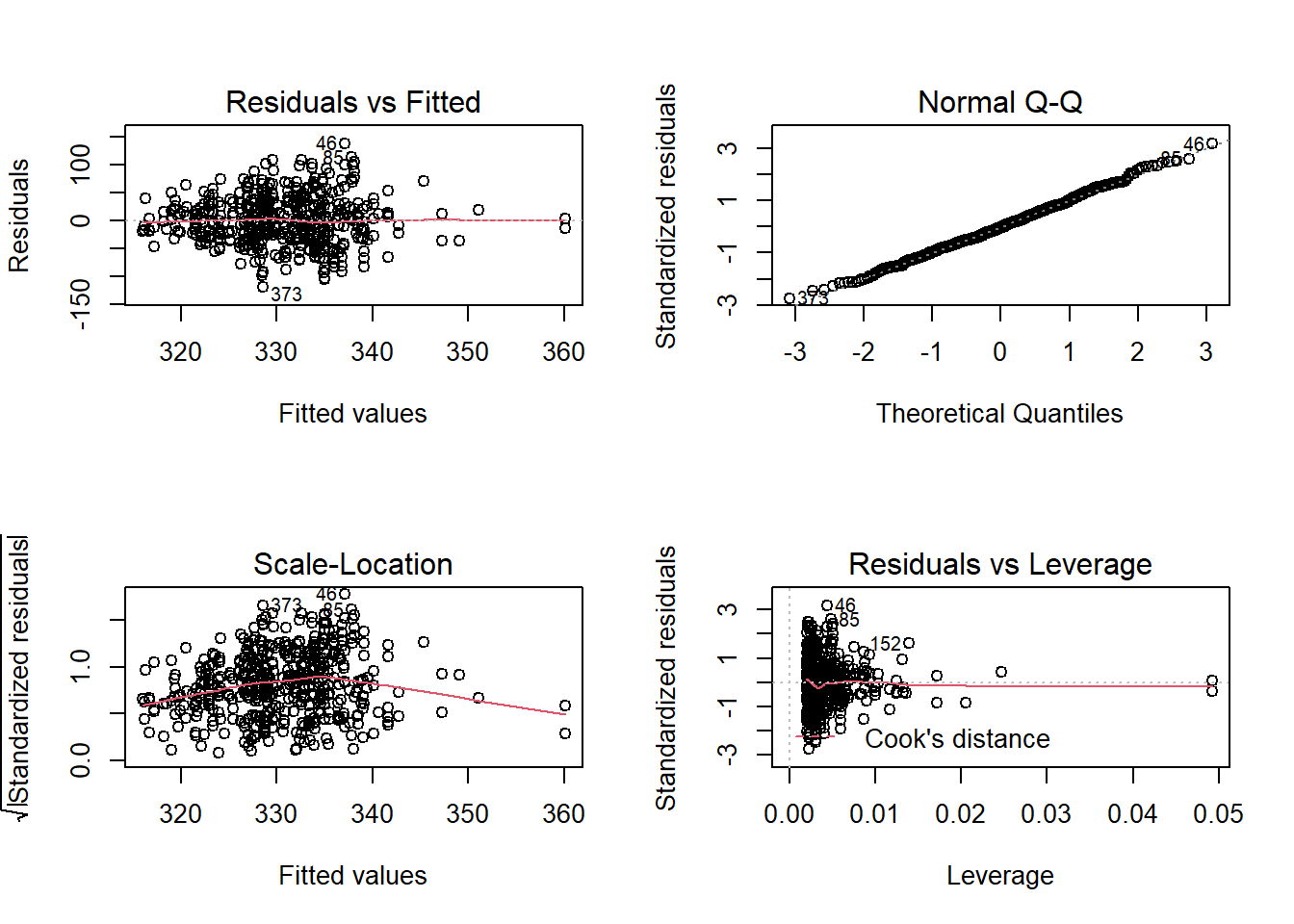
Je vous renvoie aux cours de stats pour ces évaluations spécifiques comme ce site discutant des diagnostiques d’un objet glm ou bien sur le cours PTM6675 …
Je ne parlerai pas non plus de validation interne/externe des modèles => il y a des très bon cours pour cela!!!
1.2.2.2 Pour aller plus loin visuellement
Pour aller plus visuellement dans l’évaluation du modèle on peut aussi regarder directement à loisir ce que nous avons dans nos prédictions vs la réalité des données observées (essayer notamment de mieux visualiser nos prédictions par exemple). Je vais utiliser la fonction augment() du paquet broom.
#utilise broom le paquet que j'utlise pour visualiser les erreurs plus facilement qu'avec plot(lm_objet)
m_1_augment <- augment(m_1) #ici je crée juste mon modèle avec mes prédictions pour des fins d'illustration
head(m_1_augment)## # A tibble: 6 x 9
## carc_wt days .fitted .se.fit .resid .hat .sigma .cooksd .std.resid
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 284. 99 322. 3.34 -38.5 0.00590 43.5 0.00234 -0.887
## 2 358. 315 338. 3.10 20.1 0.00509 43.6 0.000549 0.463
## 3 293. 99 322. 3.34 -29.4 0.00590 43.5 0.00136 -0.678
## 4 291. 158 326. 2.37 -35.6 0.00296 43.5 0.000994 -0.819
## 5 395. 195 329. 2.02 65.3 0.00215 43.5 0.00244 1.50
## 6 372. 164 327. 2.29 44.9 0.00277 43.5 0.00148 1.03Ici j’ai mes observations et mes prédictions ainsi que mes indicateurs de fit. Le but est de bien voir ce qui correspond aux validations des assomptions de notre modèle. Je regarde la différence entre ma prédiction et mes observations (en espérant que les résidus de mon modèle soit distribués normalement.
ggplot(m_1_augment, aes(days, carc_wt)) +
geom_point() +
stat_smooth(method = lm, se = FALSE) +
geom_segment(aes(xend = days, yend = .fitted), color = "red", linetype="dashed", size = 0.1) + theme_bw()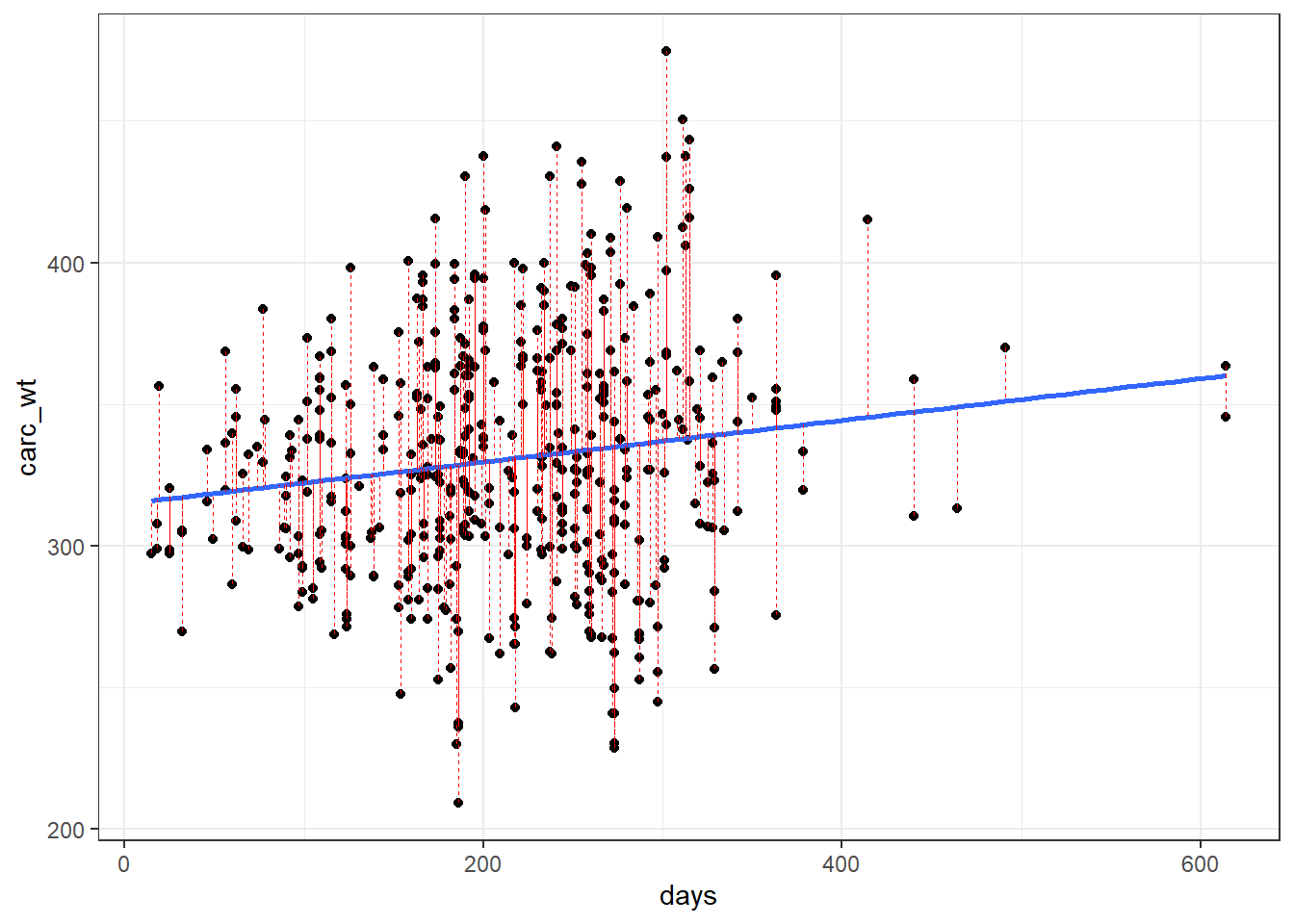
Chaque trait rouge correspond à l’erreur \(\epsilon_{i}\) de l’observation i, soit la distance \(Ypred-Yobs\).
Je peux bien sûr regarder la distribution de mes résidus dans mon modèle.
ggplot(m_1_augment, aes(x=.resid))+geom_density(size=2, color="darkblue") + theme_classic()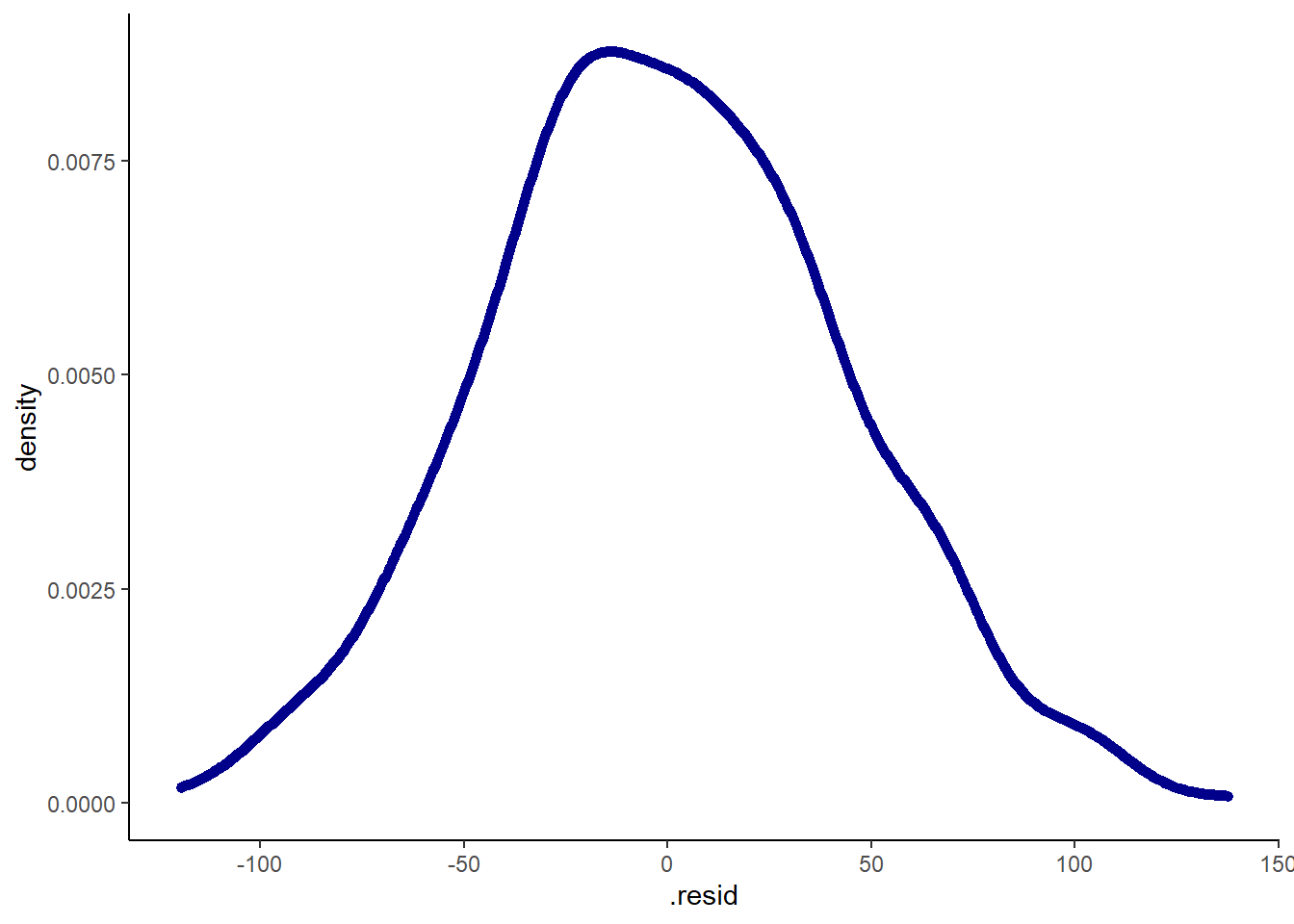
Bon c’est quand même très bien non? En tout cas moi cela me va pour me dire que je ne me casserai pas trop la tête pour transformer la variable days dans cette base de données…
Donc vous avez fait votre première régression linéaire sur R!!!
Comme avec ggplot2, le plus important était de briser la glace…
Maintenant on construit à partir de cela (et une fois que vous avez compris le principe, vous pouvez vous même avancer et faire de choses plus complexes).
Notez en revanche que tout comme dans Molière et son Bourgeois gentilhomme qui fait de la prose sans s’en rendre compte, vous avez déjà fait de la régression linéaire sans vous en rendre compte

Le Bourgeois Gentilhomme: réplique de M Jourdain
Lorsqu’on utilise method="lm" dans ggplot2 on utilise exactement la même technique (sans voir les mathématiques en arrière)
Ainsi la commande ci-dessous vous donne le même aspect que précédemment!!!
ggplot(beef, aes(x=days, y=carc_wt))+geom_point() +geom_smooth(method="lm", color="red", se=FALSE)+theme_bw()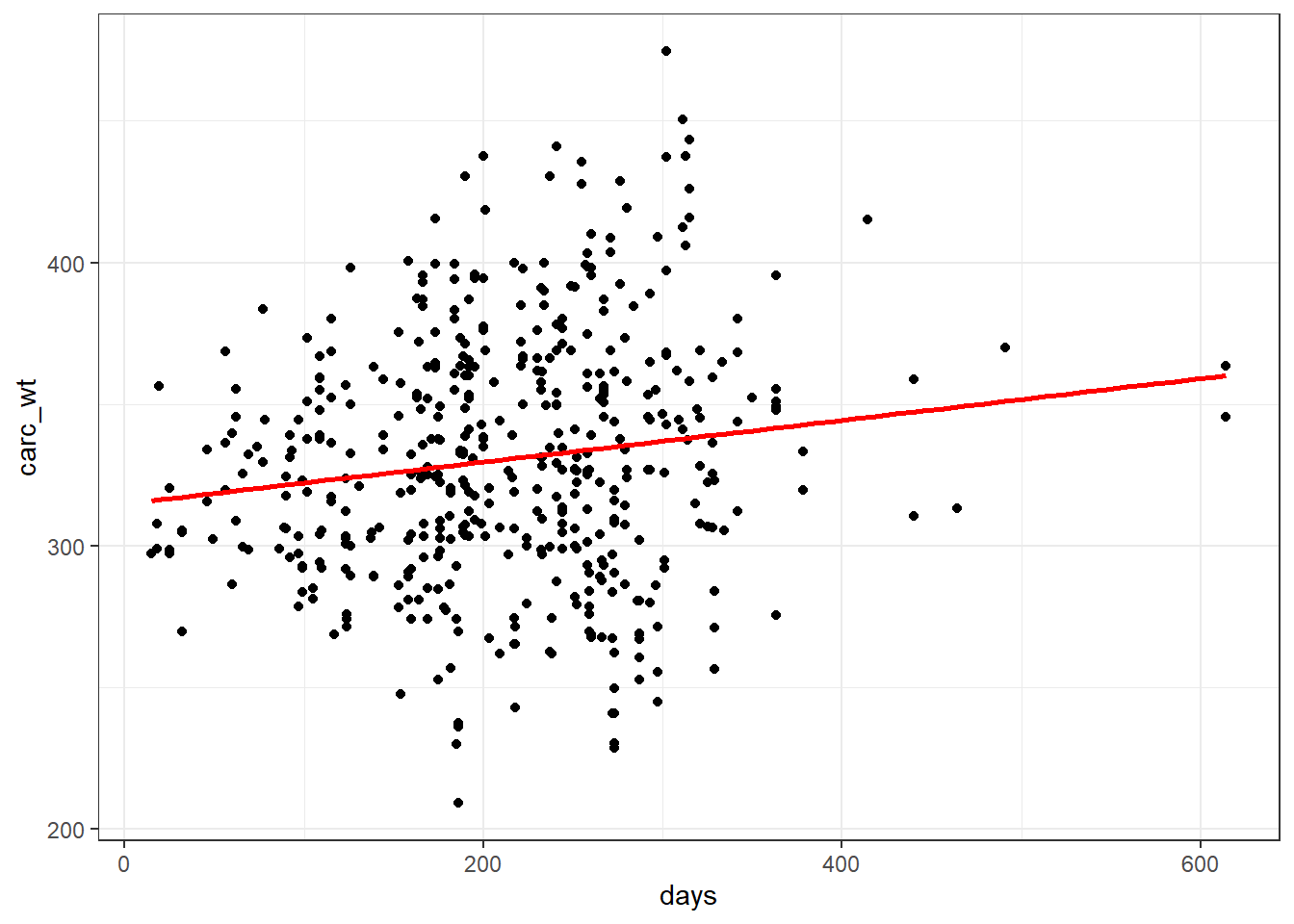
1.2.3 Variable indépendante catégorique
On l’a dit précédemment: notre base de données comprend des informations concernant des variables non continues qui peuvent être ordinale (ex : grade qui est le grade de la carcasse) ou non ordinales (breed).
Il serait intéressant de voir comment on peut évaluer leur effet sur carc_wt.
Commençons d’abord par recoder ces variables dans une nouvelle base de données beef1 afin de ne pas altérer la BD originale… (j’aurai pu aussi recoder directement dans la BD originale).
beef1 <- beef %>% mutate(race=as.factor(breed), classif=as.factor(grade))
levels(beef1$race)## [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14" "15"levels(beef1$classif)## [1] "1" "2" "3"L’ordre fait du sens pour la variable classif mais pas nécessairement pour la variable race que je voudrais par exemple regrouper par type de race (choix totalement arbitraire mais à des fins d’illustration).
#Moment du choix arbitraire de regroupement...
levels(beef1$race) <- list("Boucherie_1"=c("1", "2", "3", "4"), "Boucherie_2"=c("5", "6", "7", "8"), "Boucherie_3"=c("9", "10", "11", "12", "13", "14", "15"))
levels(beef1$race)## [1] "Boucherie_1" "Boucherie_2" "Boucherie_3"Je peux tout d’abord évaluer visuellement ce que me disent mes données avec un petit violin plot par exemple (vous savez que je suis un pro-violin plot)…
ggplot(beef1, aes(y=carc_wt,x=classif, fill=classif))+geom_violin(alpha=0.5, draw_quantiles = c(0.25, 0.5, 0.75)) + theme_bw()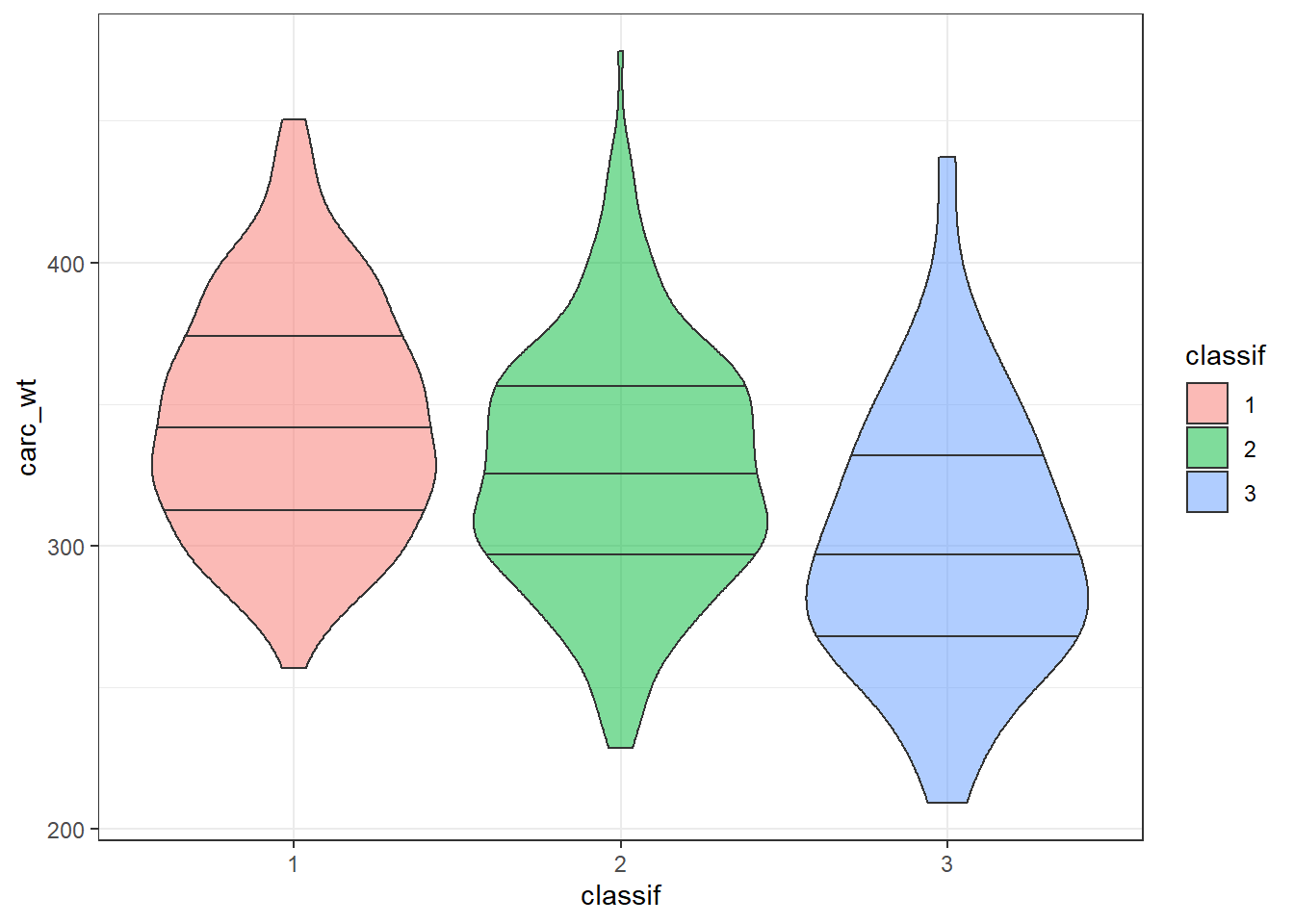
Visuellement on voit une tendance (le poids est plus faible pour les classifications plus élevées) mais bon il faut quantifier cet effet…

Ne pas juste se fier à ses yeux
L’étape suivante est donc de quantifier cet effet par un nouveau modèle linéaire m_2.
m_2 <- lm(data=beef1, carc_wt~classif)
summary(m_2)##
## Call:
## lm(formula = carc_wt ~ classif, data = beef1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -98.495 -29.859 -1.868 29.459 147.414
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 344.595 3.296 104.546 < 2e-16 ***
## classif2 -17.464 4.159 -4.199 3.19e-05 ***
## classif3 -43.232 7.043 -6.139 1.74e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 42.21 on 484 degrees of freedom
## Multiple R-squared: 0.07979, Adjusted R-squared: 0.07599
## F-statistic: 20.98 on 2 and 484 DF, p-value: 1.823e-091.2.3.1 Interprétation du modèle
Mais comment interpréter cela?
Nous avons fourni 3 catégories de classif mais nous n’avons que 2 résultats. Pourquoi?
En fait, lorsque l’on fourni une variable à \(n\) catégories l’analyse génère \((n-1)\) prédicteurs pour décrire cette variable tel qu’illustré ci-dessous pour codifier small, medium et large dans l’exemple ci-dessous:

Codage des variables catégoriques
Donc par défaut dans notre exemple le référent est la variable qui sert de comparatif pour créer les \((n-1)\) covariables (ici \(3-1=2\)). Au départ nous voulions construire le modèle :
\[Y= b_{0} + b_{1}{classif} + \epsilon\ \] Le modèle qui est généré correspond à :
\[Y= b_{classif=1} + b_{1}X_{1:classif=2} + b_{3}X_{2:classif=3} + \epsilon\ \] Si un veau est de classif=1 à ce moment là \(X_{1}=0\), \(X_{2}=0\) donc je reviens à l’intercept du modèle \(b_{classif=1}\)
Si un veau est de classif=2, alors \(X_{1}=1\) et \(X_{2}=0\) donc \(Y=b_{classif=1} + b_{1}\)
Si un veau est de classif=3, alors \(X_{1}=0\) et \(X_{2}=1\) donc \(Y= b_{classif=1} + b_{3}\)
Bref on doit se rappeler que dans ce cas notre intercept nous donne une idée du \(Y\) prédit pour notre niveau de référence de notre covariable carégorique.
Il est donc important d’être sur que l’on a définit notre animal référent comme ayant du sens d’un point de vue clinique et/ou scientifique (car c’est lui que prédira notre intercept)
Si je reviens à mon modèle:
summary(m_2)##
## Call:
## lm(formula = carc_wt ~ classif, data = beef1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -98.495 -29.859 -1.868 29.459 147.414
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 344.595 3.296 104.546 < 2e-16 ***
## classif2 -17.464 4.159 -4.199 3.19e-05 ***
## classif3 -43.232 7.043 -6.139 1.74e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 42.21 on 484 degrees of freedom
## Multiple R-squared: 0.07979, Adjusted R-squared: 0.07599
## F-statistic: 20.98 on 2 and 484 DF, p-value: 1.823e-09L’intercept correspond aux poids des animaux ayant des carcasses=1 et est signficativement différent de 0 (P\(<2*10^{-16}\)).
La classification 2 par rapport à la classification 1 a un effet négatif de 17.46 kg (P\(=3.2*10^{-5}\))
La classification 3 par rapport à la classification 1 a un effet négatif de 43.23 kg (P\(=1.74*10^{-9}\))
De façon analogue je peux regarder les diagnostiques de mon modèle:
par(mfrow = c(2, 2))
plot(m_2)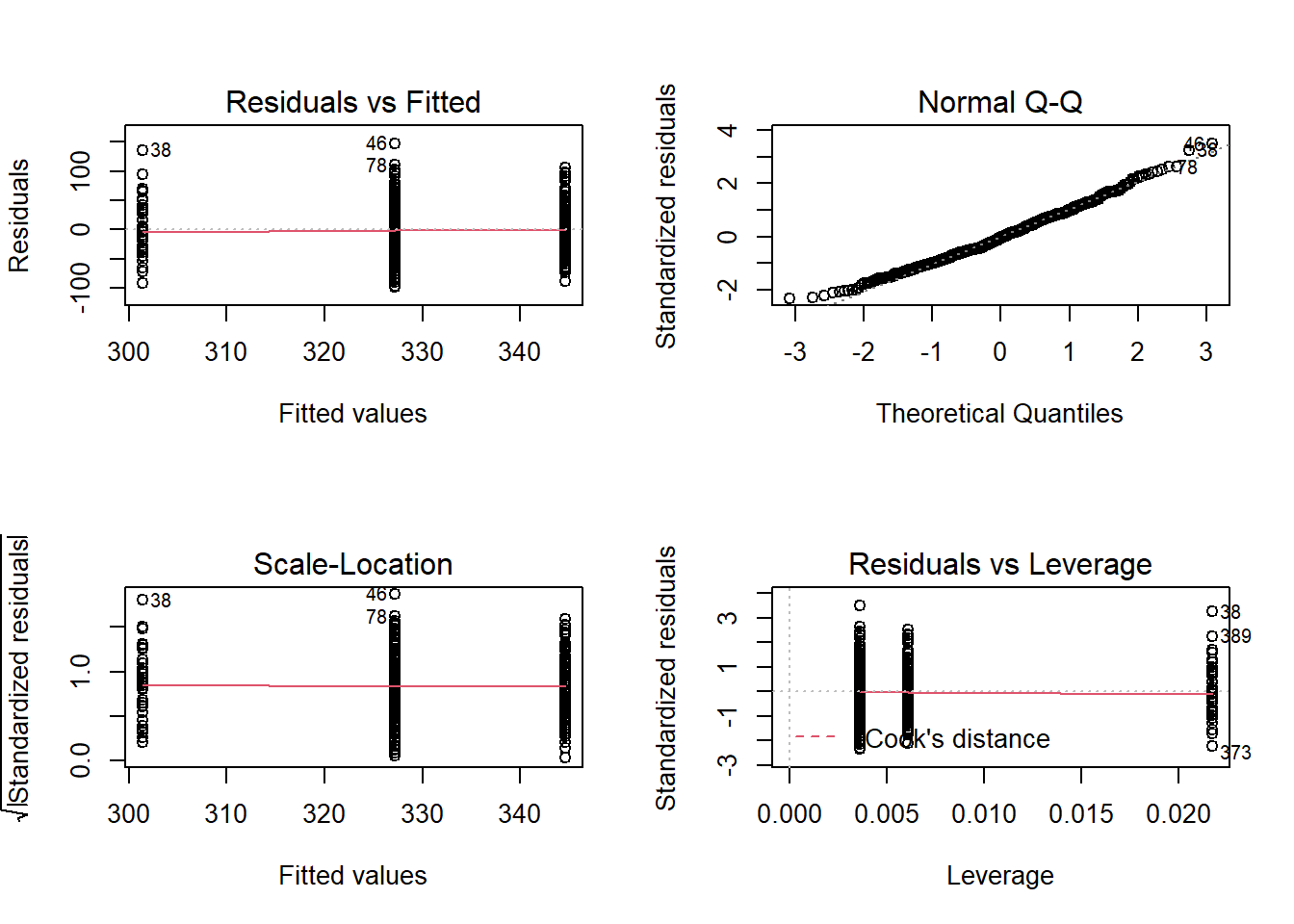
1.3 Analyse avec plusieurs variables
1.3.1 Corrélation entre les variables de la base de données
Comme on l’a dit il est important de s’assurer que les variables (\(x\)) que l’on met comme variables potentielles pour expliquer notre \(Y\) sont des variables qui ne sont pas corrélées trop fortement ou colinéaires.
Pourquoi c’est important???
dans mon modèle: \[Y= \sum_{i=1}^{N} b_{i}x_{i} + \epsilon\ \]
pour interpréter ce dernier : l’effet d’augmentation d’une unité d’un de mes \(x_{i}\) sur mon \(Y\) est de \(b_{i}\) lorsque je contrôle pour mes autres \(\overline{x_{i}}\). Cela revient donc à quantifier l’effet de mon \(x_{i}\) indépendemment des autres covariables.
Si par exemple \(x_{i}\) est très corrélé à \(x_{j}\) à ce moment là je ne peux plus dire que je peux faire cette interprétation. Dans mon modèle je vais alors avoir beaucoup d’instabilité et de variabilité de mes \(b_{i}\) si j’ai 2 variables très corrélées. On va alors parler d’inflation importante de la variance de mon modèle
Allez voir cela plus spécifiquement ou sur le site d’Ewen Gallic
Donc lorsque je sais que j’ai des variables corrélées il faut en choisir juste une des 2 pour mettre dans le modèle multivarié afin de bien s’assurer de la validité de notre modèle.
A partir de quel niveau on s’inquiète?
Bonne question!!!
Il n’y a pas à ma connaissance de seuil réellement validé. Cependant dès que les corrélations de Pearson ou de Spearman sont > 0.6 on se pose la question…
Comment évaluer les corrélations entre mes variables lorsqu’elles sont ordinales ou numériques?
Encore une fois je vous réfère au site stdha qui est une superbe ressource visuelle pour cette évaluation (ou cet autre site).
Très simplement je crée ma matrice de corrélation M avec la fonction cor pour laquelle j’ai juste spécifié ma méthode de calcul (par défaut méthode non paramétrique de Spearman):
M <- cor(beef, method = "spearman")
M## farm id grade breed sex
## farm 1.00000000 0.9819534166 0.0942927902 -0.047267740 -0.054887635
## id 0.98195342 1.0000000000 0.0994309502 -0.049781814 -0.027864129
## grade 0.09429279 0.0994309502 1.0000000000 -0.020371436 0.040146450
## breed -0.04726774 -0.0497818137 -0.0203714358 1.000000000 -0.001104455
## sex -0.05488763 -0.0278641295 0.0401464502 -0.001104455 1.000000000
## bckgrnd -0.35218911 -0.3458333001 -0.3065354229 0.195970577 0.063441033
## implant -0.12974279 -0.1224363968 0.0085993057 -0.079140755 0.338611422
## backfat 0.01311576 -0.0001836447 -0.0506662180 -0.044762619 -0.129924689
## ribeye -0.22897080 -0.2335629611 0.0002942304 0.153248824 0.050814828
## imfat -0.00970703 -0.0237959535 -0.2327685998 -0.076894479 -0.196974779
## days 0.16876996 0.1715565171 -0.0723090668 -0.035371771 -0.021212560
## carc_wt -0.20673732 -0.2000041351 -0.2657978345 0.189653909 0.465319999
## bckgrnd implant backfat ribeye imfat
## farm -0.35218911 -0.129742790 0.0131157571 -0.2289707950 -0.00970703
## id -0.34583330 -0.122436397 -0.0001836447 -0.2335629611 -0.02379595
## grade -0.30653542 0.008599306 -0.0506662180 0.0002942304 -0.23276860
## breed 0.19597058 -0.079140755 -0.0447626190 0.1532488244 -0.07689448
## sex 0.06344103 0.338611422 -0.1299246891 0.0508148283 -0.19697478
## bckgrnd 1.00000000 -0.261473360 0.1420411081 0.3444786977 0.13421042
## implant -0.26147336 1.000000000 -0.1881897194 -0.2698806872 -0.19858582
## backfat 0.14204111 -0.188189719 1.0000000000 0.4529610510 0.29379572
## ribeye 0.34447870 -0.269880687 0.4529610510 1.0000000000 0.02101070
## imfat 0.13421042 -0.198585816 0.2937957155 0.0210107035 1.00000000
## days -0.22857338 0.072692921 -0.3884095943 -0.4236784381 -0.17543519
## carc_wt 0.33856811 0.042153342 -0.2187929562 0.2400354301 -0.18487263
## days carc_wt
## farm 0.16876996 -0.20673732
## id 0.17155652 -0.20000414
## grade -0.07230907 -0.26579783
## breed -0.03537177 0.18965391
## sex -0.02121256 0.46532000
## bckgrnd -0.22857338 0.33856811
## implant 0.07269292 0.04215334
## backfat -0.38840959 -0.21879296
## ribeye -0.42367844 0.24003543
## imfat -0.17543519 -0.18487263
## days 1.00000000 0.12356408
## carc_wt 0.12356408 1.00000000 #je peux vouloir différentes méthodes ex: method= c("pearson", "kendall", "spearman")Tout est présent ici mais c’est pas super beau…
si je veux ajouter du beau pour les yeux je peux utiliser le paquet corrplot.
Le but est encore une fois de visualiser pour mieux comprendre et expliquer…
library(corrplot)
corrplot.mixed(M)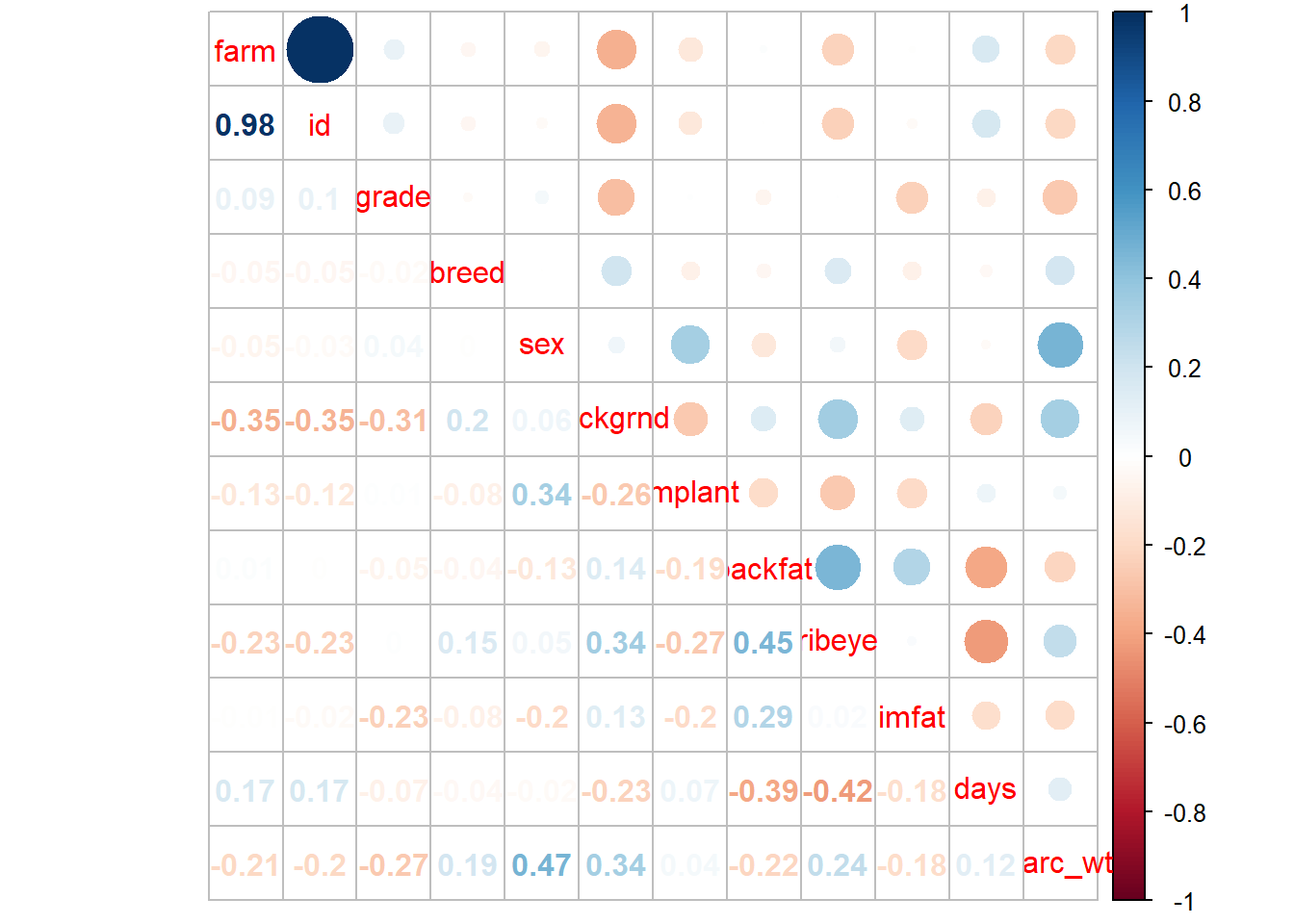
On voit ici que les corrélations sont faibles généralement donc pas de problème ici. Notez aussi que je n’ai pas retravaillé l’aspect du graph et de l’apparence…
Cependant notez bien que certains coefficients ne veulent rien dire (ex farm ou id). J’aurai pu sélectionner spécifiquement mes variables d’intérêt à tester en excluant celles dont le coefficient de Spearman n’a aucun intéret.
Ci-dessous je vais donc essayer d’avoir quelque chose qui soit plus joli à présenter ou publier..
correl <- beef %>% dplyr::select(grade, backfat, ribeye, imfat, days, carc_wt)
M_r <- cor(correl, method = "spearman" )
corrplot.mixed(M_r, lower.col = "darkgray", number.cex = .7, tl.col = "black", tl.cex=.8, order = "alphabet")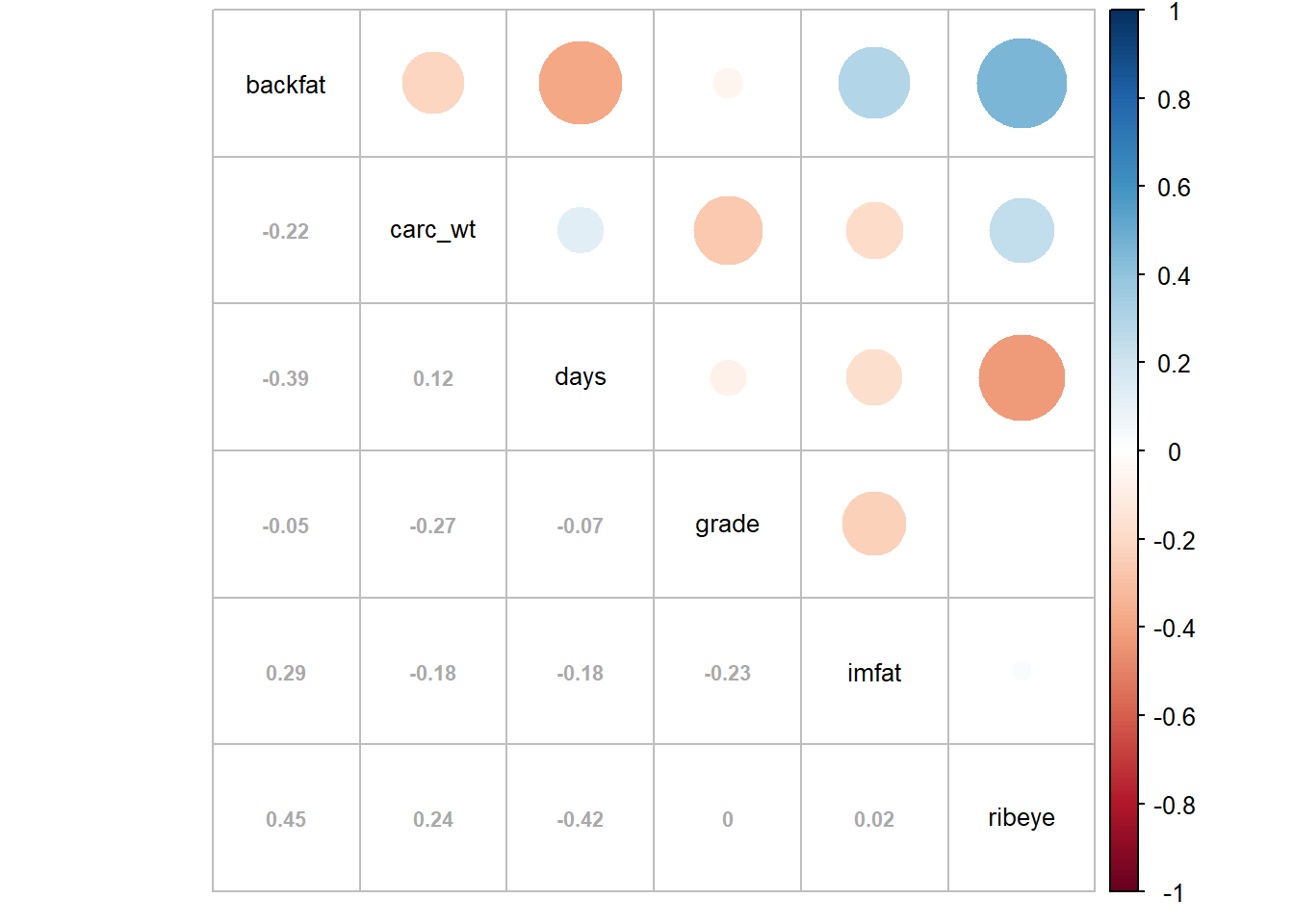
Notez ici que j’ai spécifié la taille et la couleur de mes titres et nombres…
Avec toutes les possibilités de corrplot en soi c’est déjà assez visuel (mais on peut faire beaucoup mieux…)
1.3.2 Variables catégoriques non ordinales: inflation de la variance
Il est plus difficile d’évaluer une corrélation entre des variables catégoriques non ordinale sous la forme d’une corrélation comme celle de Spearman (puisque la notion de rang sur laquelle se base cette méthode s’applique difficilement). On utilise alors dans le modèle final ce qui correspond au facteur d’inflation de la variance
Je ne m’étendrai pas là dessus mais on peut utiliser le paquet car et son argument vif. voir ce lien
1.4 Analyse multivariée
Ici encore une fois je donne un exemple mais je ne veux pas nécessairement justifier de la méthode pour le faire (il y a énormément de ressources sur comment faire un modèle multivarié). Je ne m’embarquerai donc pas dans les méthodes antégrades, rétrogrades, automatiques, validation interne et externe… Un des ouvrages qui traite de cela en long et en large est le livre d’Ewout Steyerberg: Clinical prediction model ou encore le livre Introduction to statistical learning en ligne écrit entre autre par Tibshirani l’inventeur du bootstrap
Donc, pour en revenir à notre illustration j’utilise le modèle qui évalue l’effet des variables :classif, days, race, backfat et ribeye.
Notez bien la notation avec des + entre les variables (différent de PROC REG ou autres dans SAS ou les variables sont juste ajoutées à la suite des autres)
m_max <- lm(data=beef1, carc_wt~(classif + days + race + backfat + ribeye))
summary(m_max)##
## Call:
## lm(formula = carc_wt ~ (classif + days + race + backfat + ribeye),
## data = beef1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -88.876 -26.089 0.107 22.767 126.926
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 251.55240 12.43656 20.227 < 2e-16 ***
## classif1 20.38528 3.62787 5.619 3.26e-08 ***
## classif3 -19.67648 5.88334 -3.344 0.000889 ***
## days 0.08315 0.02274 3.656 0.000285 ***
## raceBoucherie_2 -10.12427 4.68602 -2.161 0.031227 *
## raceBoucherie_3 7.32693 4.23650 1.729 0.084368 .
## backfat -14.68314 1.66365 -8.826 < 2e-16 ***
## ribeye 11.38984 1.11921 10.177 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 36.35 on 479 degrees of freedom
## Multiple R-squared: 0.3245, Adjusted R-squared: 0.3147
## F-statistic: 32.88 on 7 and 479 DF, p-value: < 2.2e-16Toutes mes variables sont associées au poids carcasse…
Je regarde ensuite les résiduels de mon modèle.
par(mfrow = c(2, 2))
plot(m_max)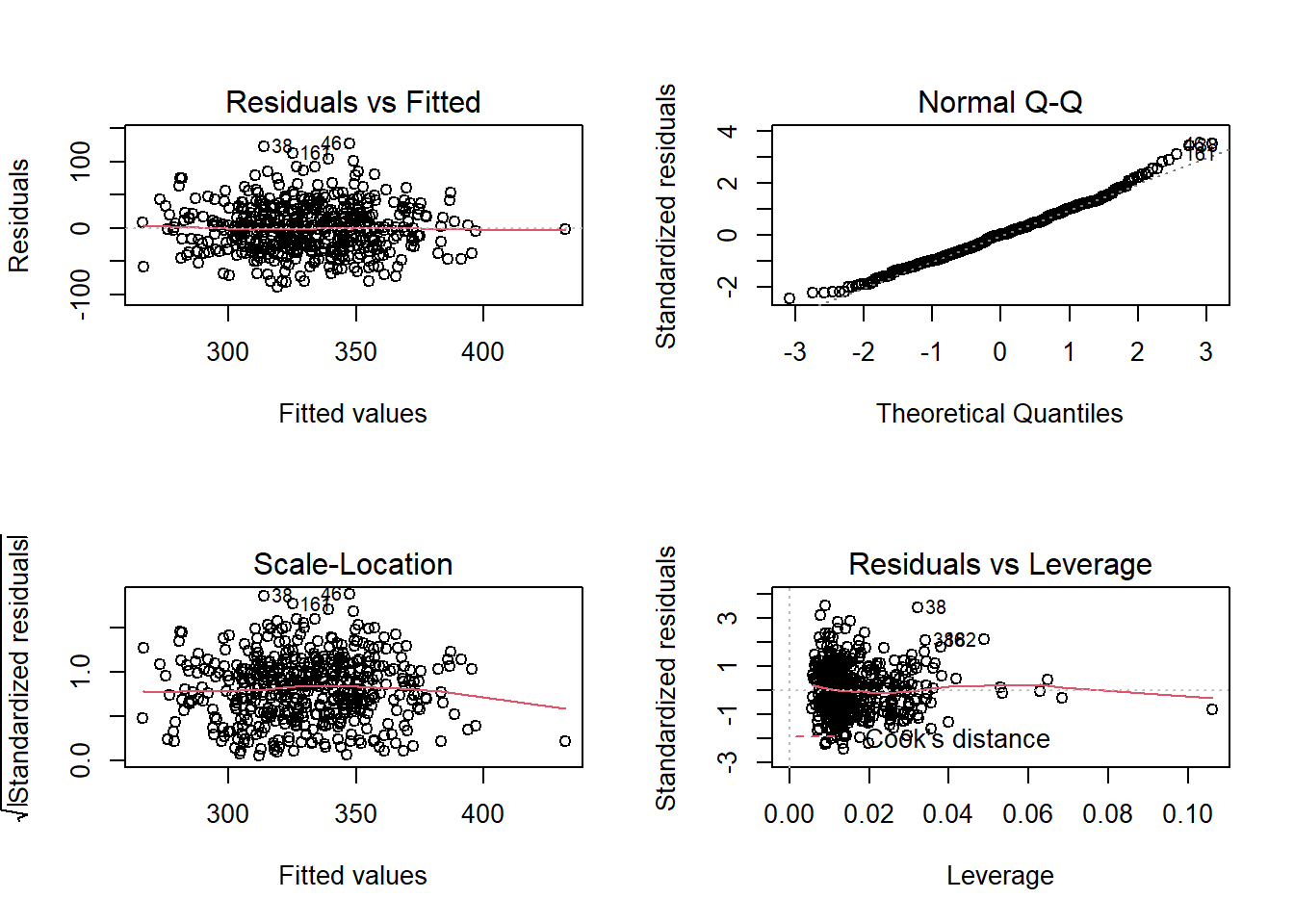
Encore une fois on est assez bon dans notre évaluation des résiduels.
1.5 Présentation des résultats
1.5.1 Présentation des coefficients du modèle
Bon, une fois qu’on a notre résultat on est content mais il faut maintenant visualiser ce que l’on a fait pour notamment permettre une meilleure compréhension lorsqu’on va expliquer cela aux utilisateurs de la recherche. J’utilise le paquet sjPlotqui est juste phénoménal!!!. On pourrait faire un tutoriel complet là dessus…
je vous réfère au site du concepteur de sjPlot Daniel Lüdecke.
Ce paquet peut vous aider dans :
1 les régressions linéaires
2 les modèles linéaires généralisés (glm)
3 les modèles hierarchiques (linéaires et glm, qu’on n’abordera pas dans ce tutoriel)
Donc dans la plupart des modèles que vous allez vouloir utiliser…
Dans un premier temps je me sers de la fonction plot_model qui ne nécessite que le nom du modèle lm que j’ai créé.
#tout simplement
plot_model(m_max)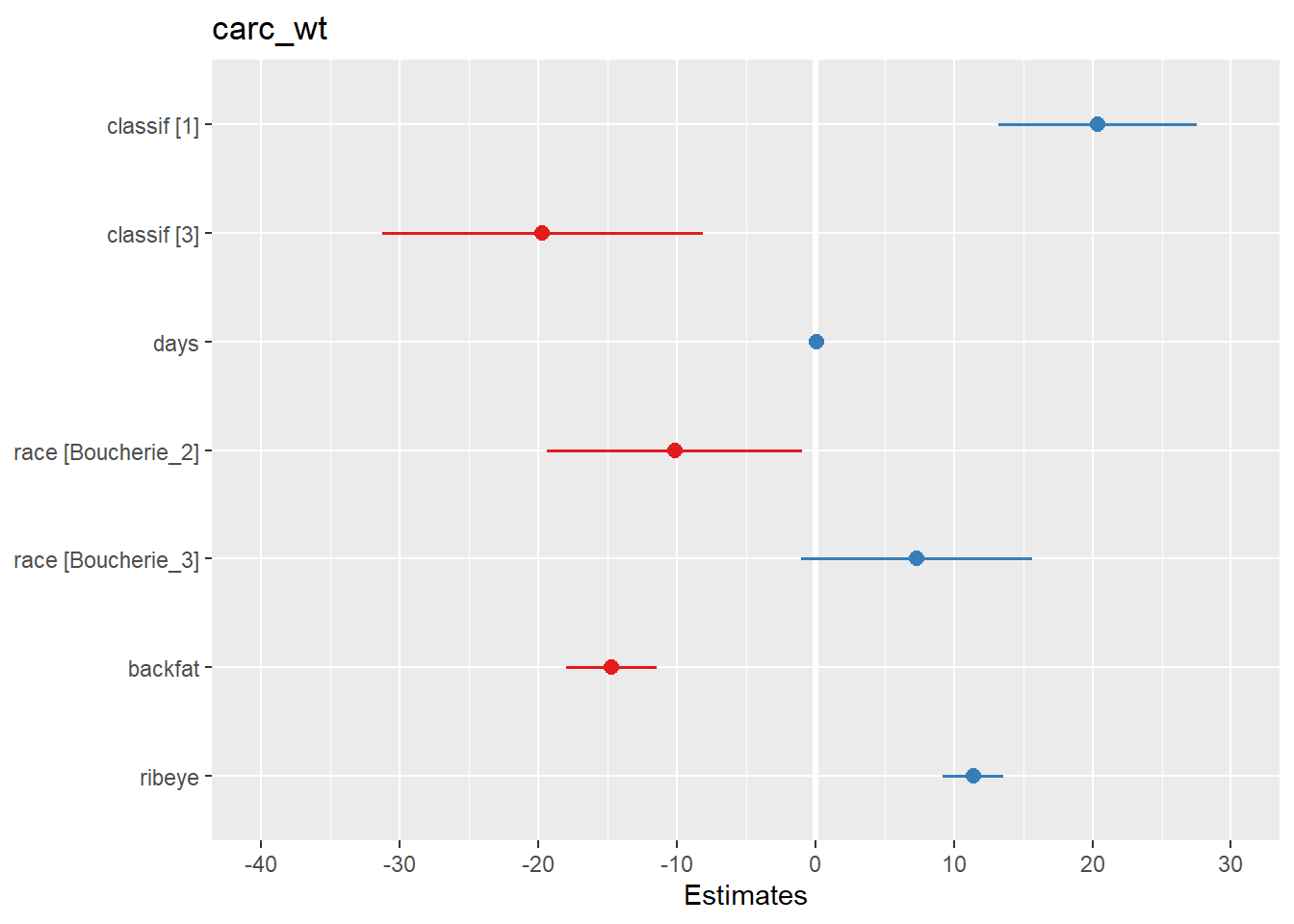
Vous voyez par défaut que ce qui est positivement associé est en bleu. Ce qui est négativement associé en rouge.
Notez que c’est un objet qui se rapproche de ggplot2 donc rien ne m’empêche d’utiliser des arguments que nous avons vus dans le tutoriel sur le sujet.
Je peux aussi changer le nom des variables, les couleurs ,les axes…
plot_model(m_max) + theme_bw() +ggtitle("visuel sympa") +labs(y="Effet sur la carcasse (kg)")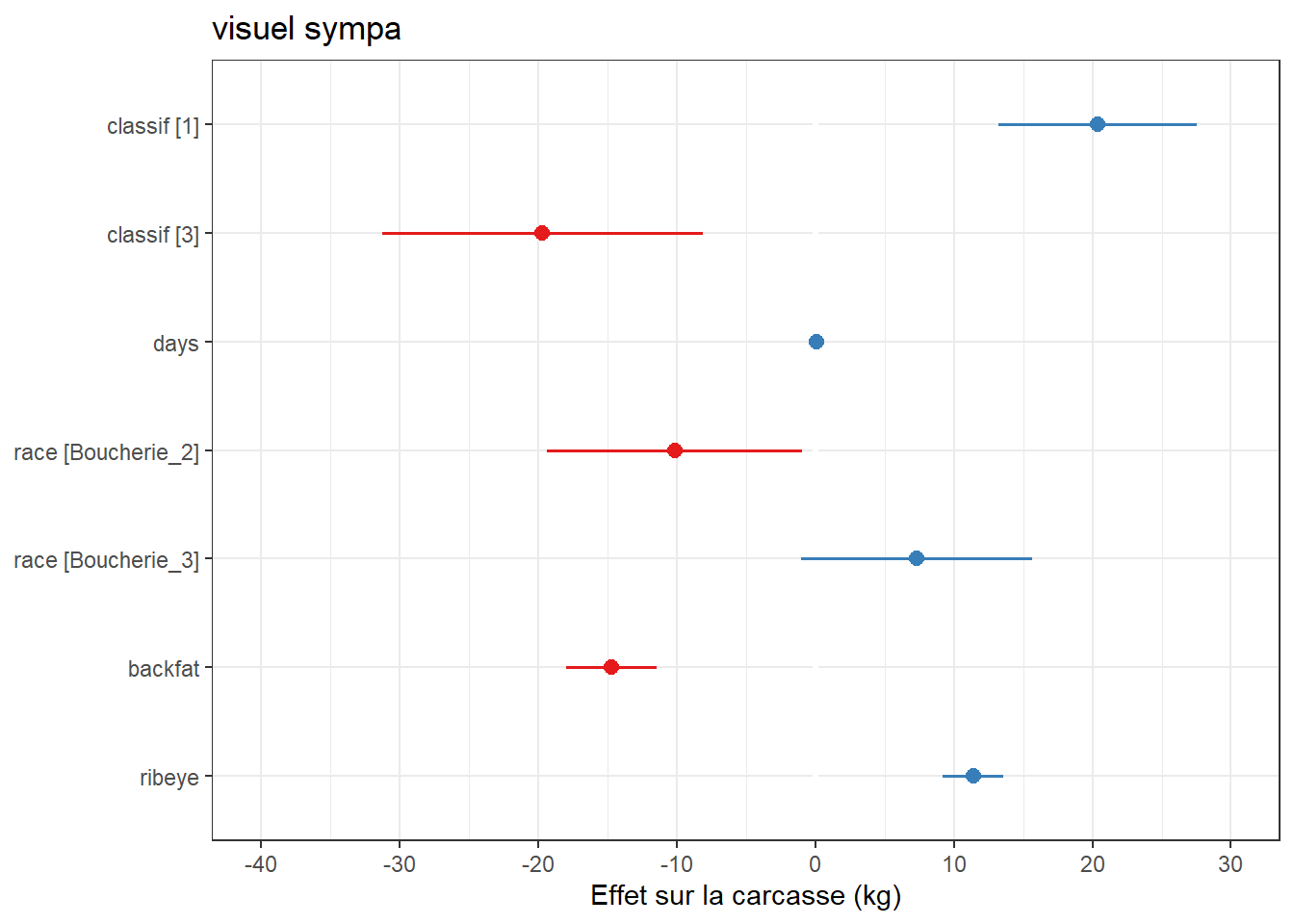
#on peut même mettre les valeurs et les niveaux de p ainsi que la ligne sans effet...
plot_model(m_max, show.values = TRUE, value.offset = .3, vline.color = "purple", width=.2) + theme_bw() +ggtitle("visuel sympa") +labs(y="Effet sur la carcasse (kg)")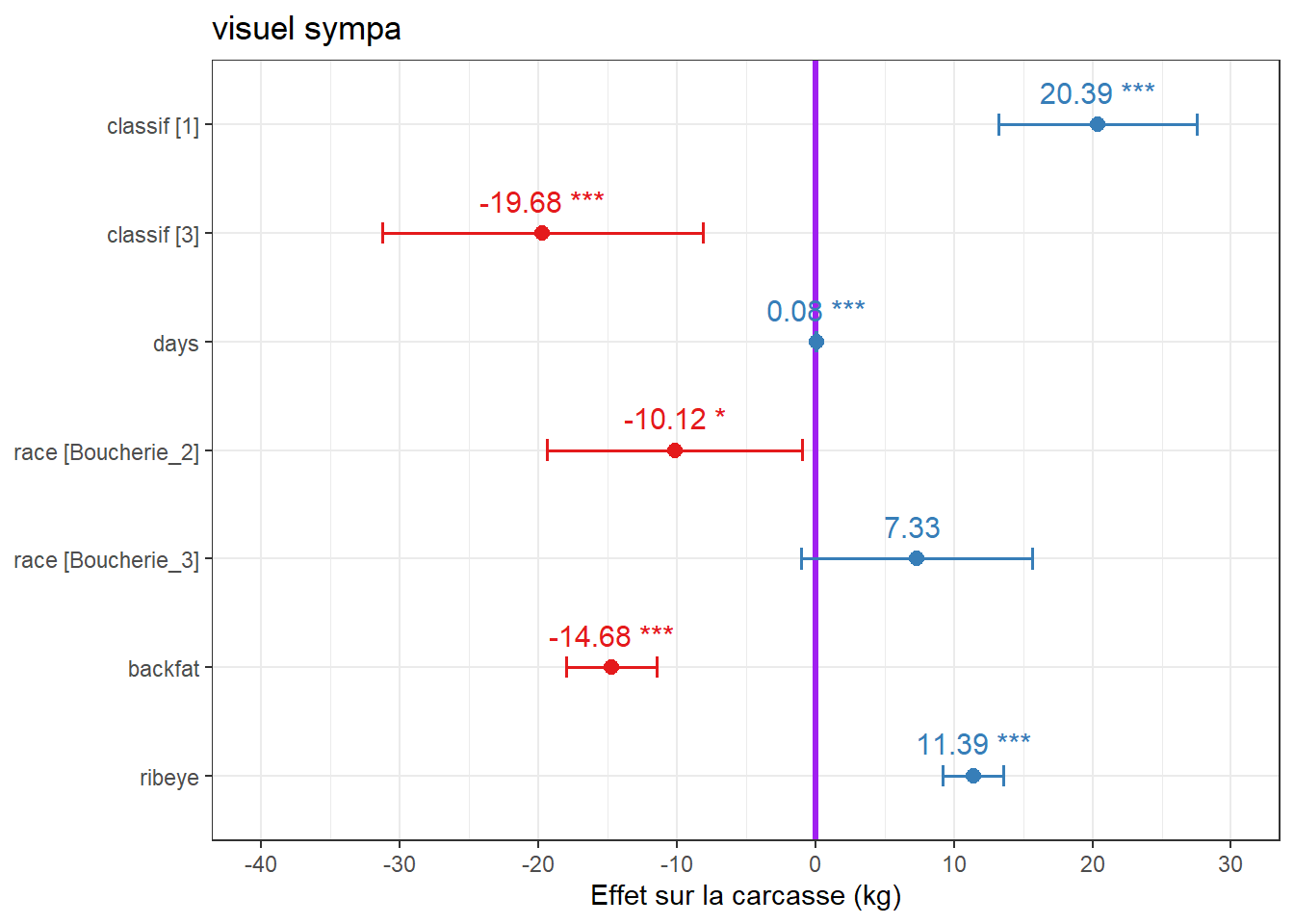

Si c’est pas beau tout cela??
1.5.2 Effets marginaux
En résumé les effets marginaux sont un peu comme les LSMeans. Ce sont les valeurs prédites de mon \(Y\) selon mes niveaux de \(x\) en tenant compte des autres prédicteurs ainsi que de l’aspect non-balancé des données (ie dans la plupart des études je ne décide pas à priori de la distribution de mes \(x\) dans mes observations…). C’est donc une façon très visuelle de voir l’effet d’une variable \(x\) sur une issue \(Y\) en contrôlant pour d’autres covariables du même modèle.
Grâce à cet effet je peux facilement interpréter l’impact des covariables sur ma prédiction.
plot_model(m_max, type = "pred", terms = "classif") + theme_classic() + labs(x="Score de carcasse", y="Poids de carcasse (kg)") + ggtitle("Effets marginaux de la classification sur le poids carcasse")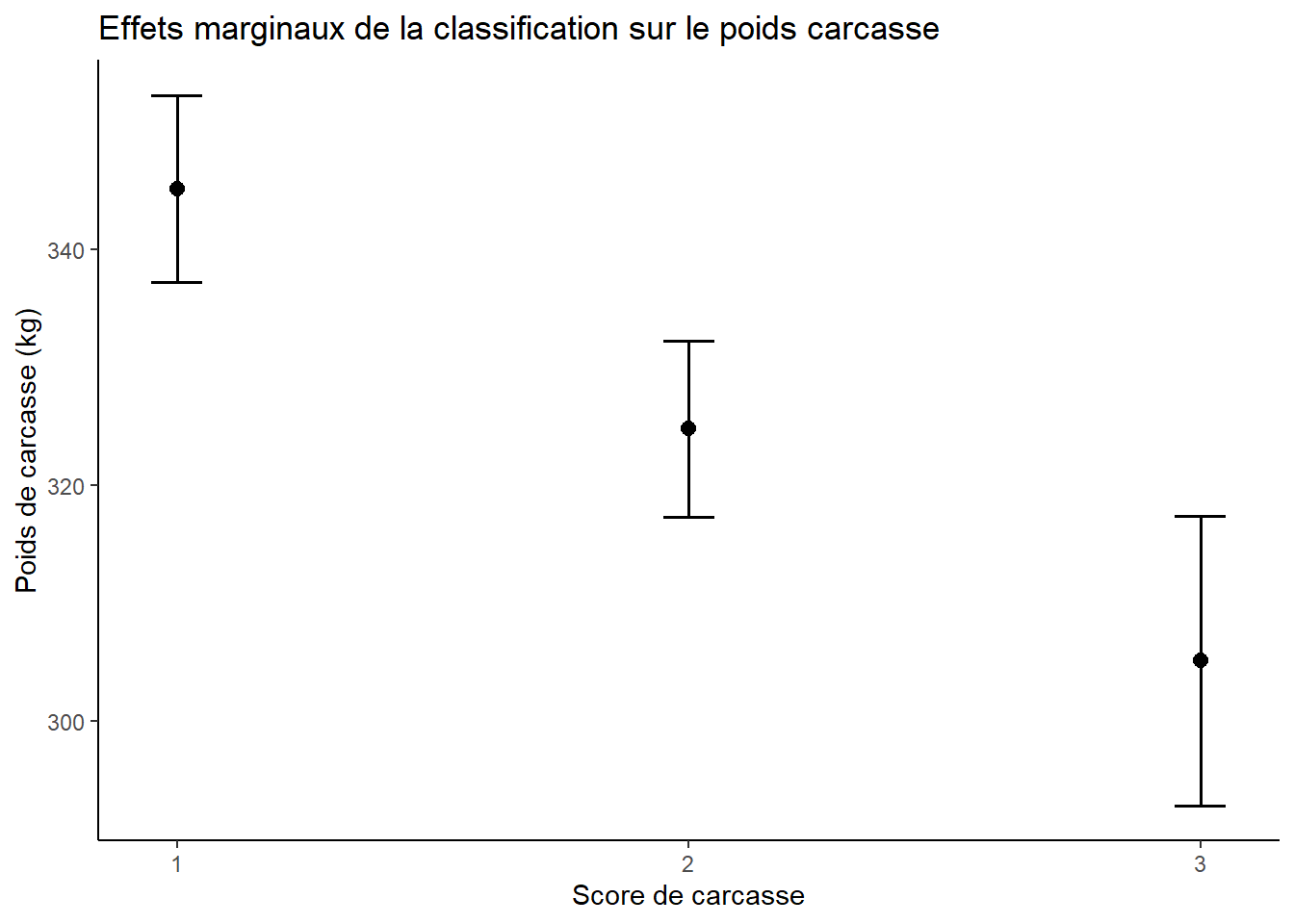
Donc ici j’ai les effets marginaux de la variable \(Y\) selon un de mes \(x\) qui était catégorique.
je vois donc très bien que le score de la carcasse est inversement corrélé à son poids
Je pourrais aussi vouloir visualiser l’effet d’une variable continue sur mon \(Y\) en contrôlant pour les autres covariables du modèle.
Par exemple, pour voir l’effet de la variable backfat sur carc_wt.
plot_model(m_max, type = "pred", terms = "backfat") + theme_bw()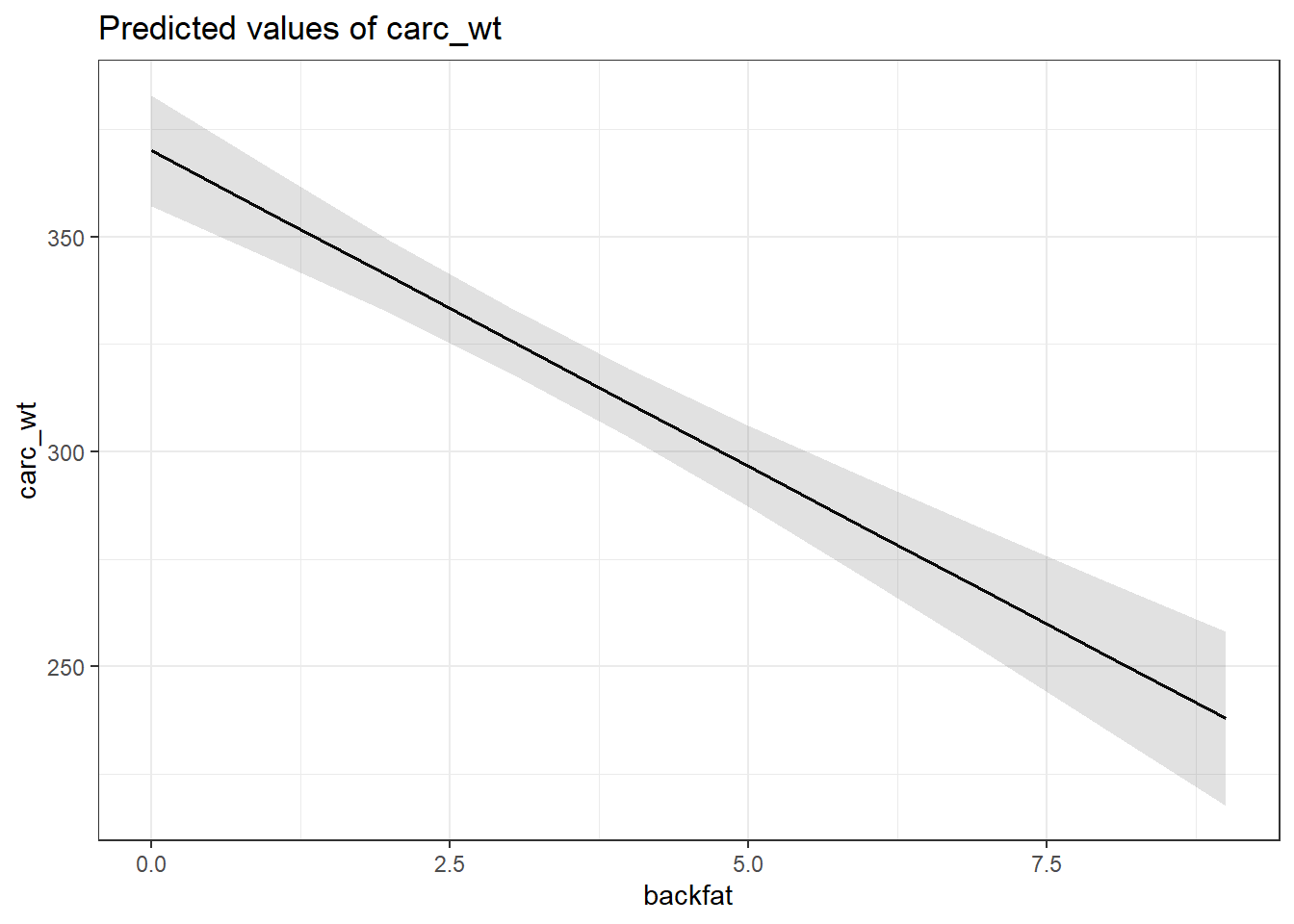
1.5.3 Comparer des modèles?
On peut aussi vouloir comparer des modèles différents plus ou moins complexe:
#exemple 1 modèle avec une interaction race*carcass
m_max_2 <- lm(data=beef1, carc_wt~(classif + days + race + backfat + ribeye +classif*race)) # un modèle avec une interaction en plus
m_max_3 <- lm(data=beef1, carc_wt~(classif + days + race + backfat)) # un modèle sans ribeyeJ’utilise la comparaison des modèles par la fonction plot_models:
plot_models(m_max, m_max_2, m_max_3) + theme_bw()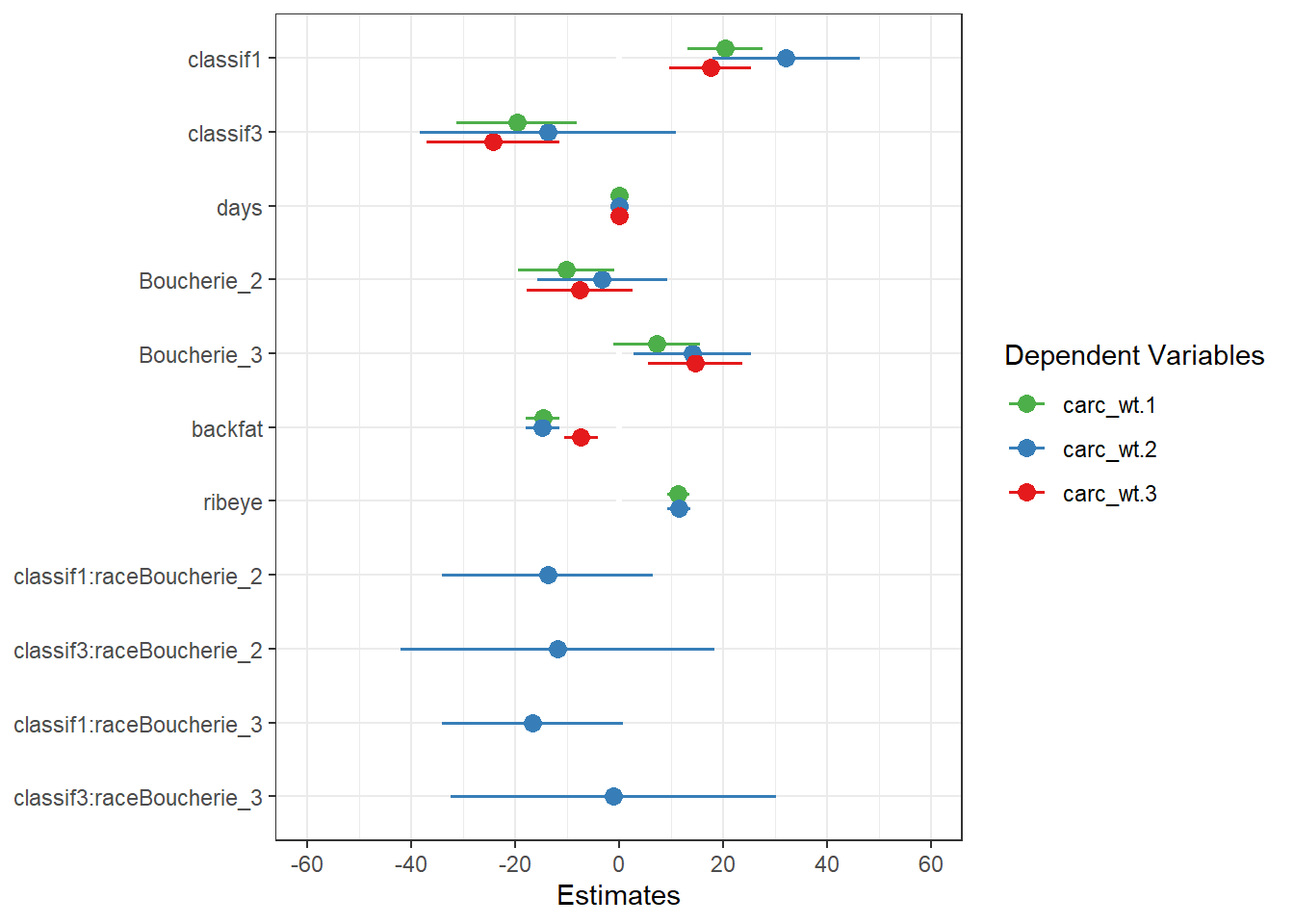
Donc je peux directement voir mes modèles ainsi que les impacts sur les coefficients…
Pour comparer des modèles je vous renvoie à d’autres cours de statistiques.
1.5.4 Visualisation des interactions
L’interaction est souvent difficile à expliquer sans un bon graphique à l’appui et encore une fois : une image vaut 1000 mots.
plot_model(m_max_2, type = "pred", terms=c("classif", "race")) +theme_classic()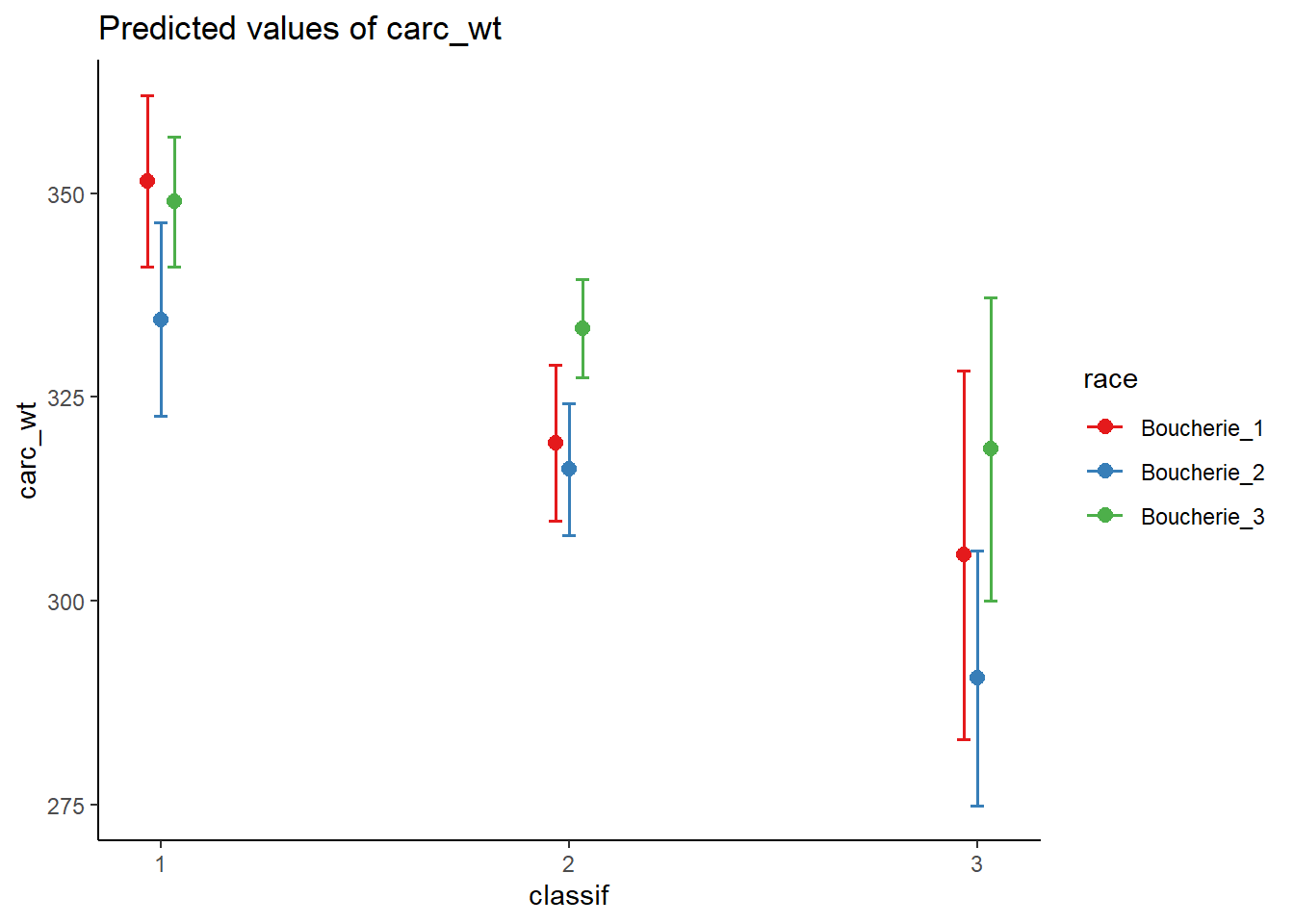
Donc ici on voit très bien l’interaction de la race vs classif sur le poids !!!
On pourrait aussi visualiser les effets d’interaction entre une variable numérique et catégorique ou entre2 variables numériques. **Je vous réfère à la portion interaction de sjPlot
Je peux également résumer tous mes modèles sous la forme d’une table:
tab_model(m_max, m_max_2, m_max_3)| carc_wt | carc_wt | carc_wt | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictors | Estimates | CI | p | Estimates | CI | p | Estimates | CI | p |
| (Intercept) | 251.55 | 227.12 – 275.99 | <0.001 | 244.23 | 218.66 – 269.80 | <0.001 | 340.53 | 321.39 – 359.68 | <0.001 |
| classif [1] | 20.39 | 13.26 – 27.51 | <0.001 | 32.14 | 17.93 – 46.35 | <0.001 | 17.53 | 9.70 – 25.36 | <0.001 |
| classif [3] | -19.68 | -31.24 – -8.12 | 0.001 | -13.73 | -38.31 – 10.86 | 0.273 | -24.24 | -36.94 – -11.54 | <0.001 |
| days | 0.08 | 0.04 – 0.13 | <0.001 | 0.09 | 0.04 – 0.13 | <0.001 | 0.02 | -0.03 – 0.07 | 0.441 |
| race [Boucherie_2] | -10.12 | -19.33 – -0.92 | 0.031 | -3.22 | -15.76 – 9.31 | 0.614 | -7.52 | -17.65 – 2.61 | 0.145 |
| race [Boucherie_3] | 7.33 | -1.00 – 15.65 | 0.084 | 14.06 | 2.73 – 25.38 | 0.015 | 14.59 | 5.55 – 23.63 | 0.002 |
| backfat | -14.68 | -17.95 – -11.41 | <0.001 | -14.69 | -17.97 – -11.41 | <0.001 | -7.34 | -10.58 – -4.09 | <0.001 |
| ribeye | 11.39 | 9.19 – 13.59 | <0.001 | 11.49 | 9.29 – 13.70 | <0.001 | |||
|
classif [1] * race [Boucherie_2] |
-13.75 | -33.98 – 6.48 | 0.182 | ||||||
|
classif [3] * race [Boucherie_2] |
-11.89 | -42.06 – 18.28 | 0.439 | ||||||
|
classif [1] * race [Boucherie_3] |
-16.59 | -33.95 – 0.77 | 0.061 | ||||||
|
classif [3] * race [Boucherie_3] |
-1.08 | -32.43 – 30.27 | 0.946 | ||||||
| Observations | 487 | 487 | 487 | ||||||
| R2 / R2 adjusted | 0.325 / 0.315 | 0.331 / 0.315 | 0.179 / 0.168 | ||||||
Donc vous voyez on a bien avancé avec cette portion!!! Pour tout ce qui est visualisation le principe va rester le même avec le package sjPlot.
FIN DE LA PORTION DE RÉGRESSION LINÉAIRE

Attention aux limites de la prédiction!!!
2 Régression logistique et modèles linéaires généralisés
La régression linéaire s’utilise pour des \(Y\) continus mais qu’en est il pour des variables qui sont par exemples dichotomiques?
On a en effet bien des cas en médecine vétérinaire où cela s’applique (on veut prédire une condition vs son contraire).

A ou B?
Cette image résume bien la régression logistique. On veut trouver un modèle avec des variables qui nous permettent de déterminer une option vs une autre (exemple mort vs survie, malade vs non-malade, gestant vs non gestant, succès ou échec…). Les exemples sont pléthoriques en médecine vétérinaire…
En fait ce que l’on cherche alors est une relation pour prédire A vs B ou B vs A selon nos spécifications. La régression linéaire n’est alors clairement pas possible (mon \(Y\) a juste 2 valeurs possibles). On va alors passer par une transformation de notre \(Y\) pour permettre de retourner à un modèle linéaire…
Je m’explique:
\[f(Y)=b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n} + \epsilon\ \] Donc en gros, on trouve le lien pour revenir à une forme linéaire… (notez que si \(f()=identité\) on revient à notre régression linéaire). On va parler de modèles linéaires généralisés (ou leur abréviation en anglais (GLM)). On trouve une fonction qui nous ramène à une droite. La difficulté supplémentaire est l’interprétation du modèle qui n’est pas directement implicite et nécessite de se ramener à \(Y\).
Donc :
\[Y=f^{-1}(b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n}+ \epsilon)\]
Pour revenir à nos variables dichotomiques à prédire on utilise la fonction logistique (logit) qui définit la probabilité de présenter l’évènement à prédire \(p(Y=A)\) ou que j’appellerai \(p\) par la suite afin d’alléger le texte.
\[logit(p)=ln(\frac{p}{1-p})\]
On y reviendra plus tard… Mais notez tout de suite l’expression entre parenthèse \(\frac{p}{1-p}\) : c’est la cote (odds) de \(p\).
Si on fait la conversion entre les 2 équations précédentes on va trouver que:
\[p=\frac{e^{b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n}}}{1+e^{b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n}}}\]
Donc à la manière d’une régression linéaire on pourra prédire la probabilité de l’issue modélisée en fonction du profil de covariable de notre animal et des coefficients de notre modèle.
Lorsque nous parlons de régression logistique on va souvent comparer le l’odds de p selon le profil de covariables…

Pourquoi la régression linéaire ne marche pas?
La fonction logistique a la forme en S caractéristique et essaie fitter le mieux possible la séparation des \(Y\). Elle est aussi bornée entre 0 et 1, contrairement à la régression linéaire qui pourrait prédire des valeurs supérieures à 1 ou inférieures à 0 ce qui ne fait pas de sens…
La façon de fitter le modèle est également différente de la régression linéaire qui utilise la méthode des moindres carrés (Ordinary Least Squares OLS). Dans le cadre de la régression logistique on utilise une méthode qui maximise la vraisemblance des données selon le modèle (Maximum Likelihood Estimation). Donc la méthode OLS regarde la méthode qui minimise les résidus tandis que la méthode MLE regarde les paramètres associés à la courbe la plus susceptible d’avoir généré les données… (Débat un peu sémantique j’en conviens pour des gens comme nous intéressés à la clinique…)
D’autres fonctions se rapprochent de la fonction logistique (modèles probit ou complementary loglog (cloglog(p)=-log(log(p))) mais je n’irai pas dans ce débat un peu trop mathématique… la régression logistique est de loin la plus fréquemment utilisée…
2.1 Évaluation de la variable dépendante
Tout d’abord je choisi une base de données en exemple tirée du livre de Ian Dohoo. Ici je vais réutiliser la BD calf afin de prédire le risque de sepsis qui est codé comme vous vous en souvenez en 0/1.
veaux <- read_excel("calf.xlsx")
head(veaux, n=7)## # A tibble: 7 x 14
## case age breed sex attd dehy eye jnts post pulse resp temp umb
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1670 5 1 1 2 12 NA 0 2 NA NA 37.6 0
## 2 8124 3 2 0 1 13.5 0 0 0 130 120 39.2 0
## 3 6954 2 3 1 2 NA 1 0 2 NA NA NA 1
## 4 2737 3 4 1 1 5 0 0 0 132 40 38.6 0
## 5 5341 3 5 0 1 0 0 0 1 128 48 38.6 1
## 6 6749 10 6 0 1 5.5 0 0 0 160 48 39.6 0
## 7 3234 4 7 0 2 7 0 1 2 180 84 39 1
## # ... with 1 more variable: sepsis <dbl>Pour des fins de reproductibilités entre les différents paquets sur la gestion des données manquantes je vais éliminer les données manquantes de la BD eu utilisant la fonction na.omit() (si vous êtes intéressés à en savoir un peu plus sur les particularités des données manquantes voir le tutoriel REMA-4)…
veaux=na.omit(veaux)Tout d’abord je veux savoir quelle est la caractéristique de la variable que je veux prédire…
freq(factor(veaux$sepsis))## Frequencies
##
## Freq % Valid % Valid Cum. % Total % Total Cum.
## ----------- ------ --------- -------------- --------- --------------
## 0 152 71.36 71.36 71.36 71.36
## 1 61 28.64 100.00 28.64 100.00
## <NA> 0 0.00 100.00
## Total 213 100.00 100.00 100.00 100.00J’ai donc environ 3 veaux sur 10 présentant cette caractéristique.
Je peux utiliser aussi la visualisation sous la forme d’un diagramme en barre.
veaux %>% ggplot(aes(x=sepsis))+geom_bar(fill="darkblue", col="yellow") + theme_bw()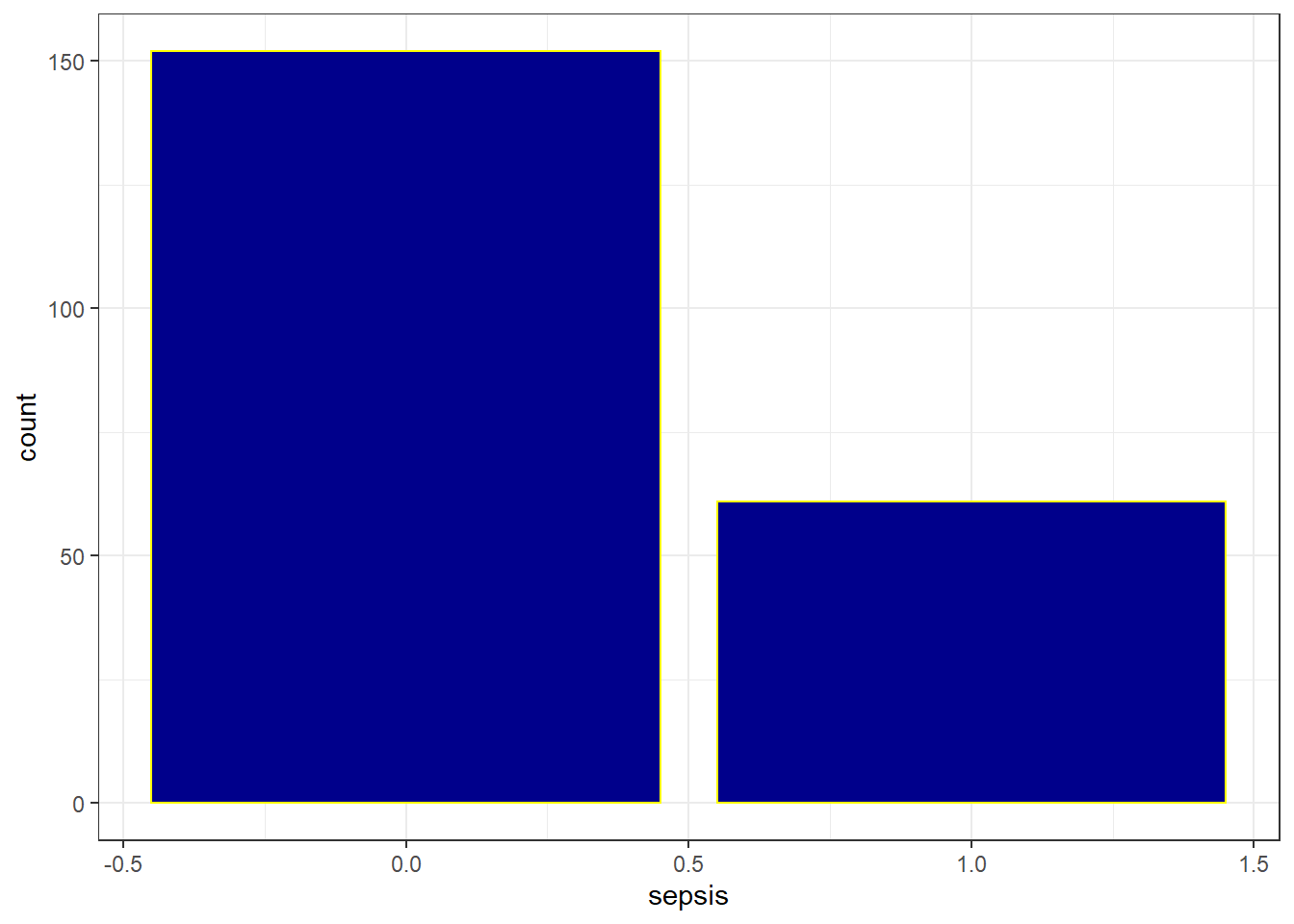
2.2 Relation avec une seule variable (analyse univariée)
Maintenant je veux regarder l’effet de la fréquence cardiaque (FC=pulse) sur ma variable dépendante (sepsis).
Tout d’abord à quoi ressemble la distribution de la FC et des autres variables continues?
Précédemment j’avais utilisé une petite requête ggplot (voir ci-dessous) pour visualiser spécifiquement ma covariable d’intérêt (la FC).
ggplot(veaux, aes(x=pulse))+geom_histogram(fill="darkblue", color="red")+theme_classic()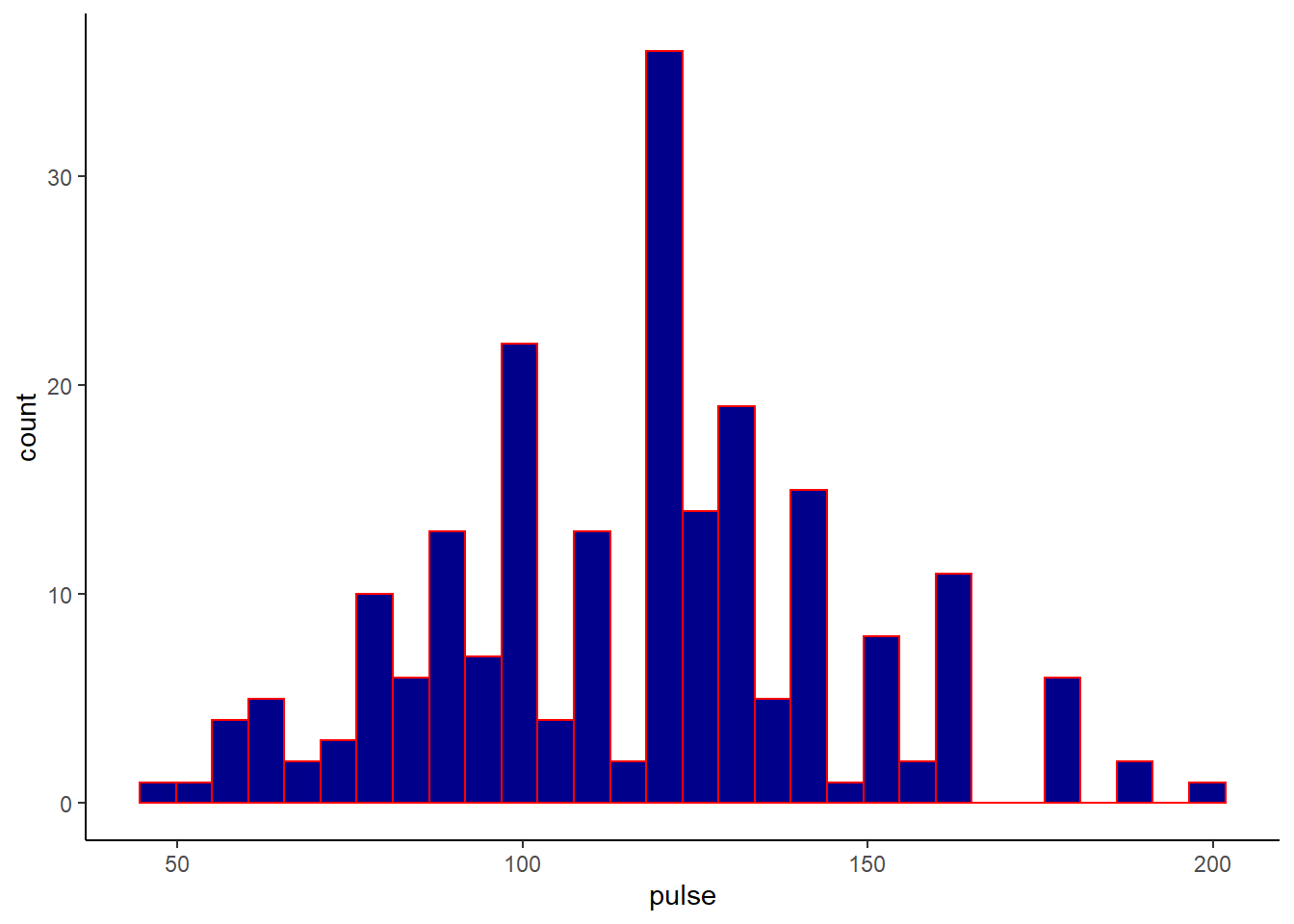
Mais je peux aussi utiliser le package funModeling. Ce paquet est un ensemble de fonctions et d’analyses qui sont dédiées à la prédiction sous la forme de régression linéaire ou GLM. Pour plus d’informations vous pouvez vous référer au site funModeling.
#fonction funModeling::plot_num()
plot_num(veaux, bins=30)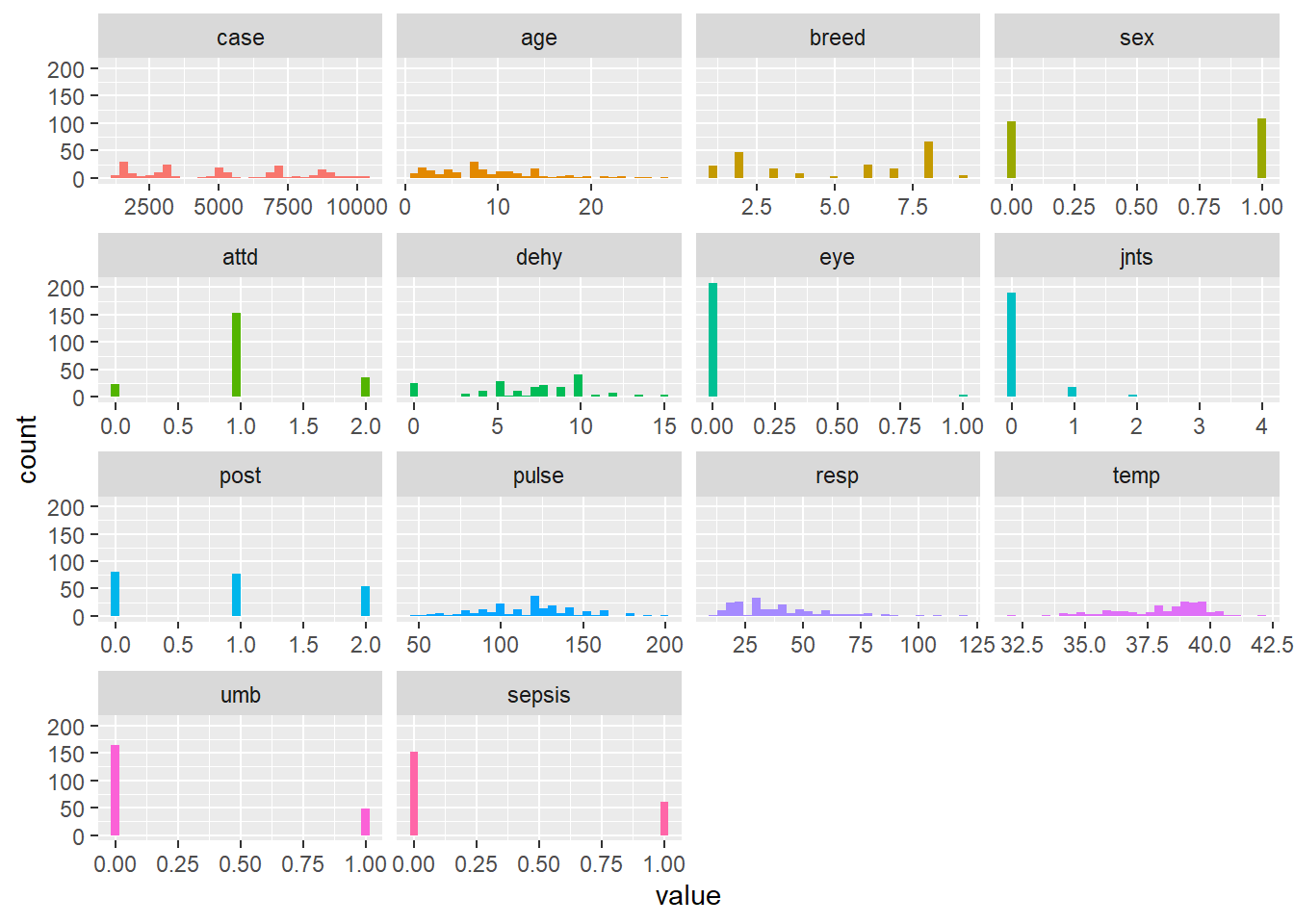
OK vous voyez le gain de temps… en un coup d’oeil je visualise toutes mes variables numériques… vous voyez aussi que de nombreuses variables sont considérées par défaut comme numériques.
On va changer cela en spécifiant ce que nous voulons voir…
veaux_s <- veaux %>% dplyr::select(dehy, pulse, resp, temp ,age)
plot_num(veaux_s, bins=20)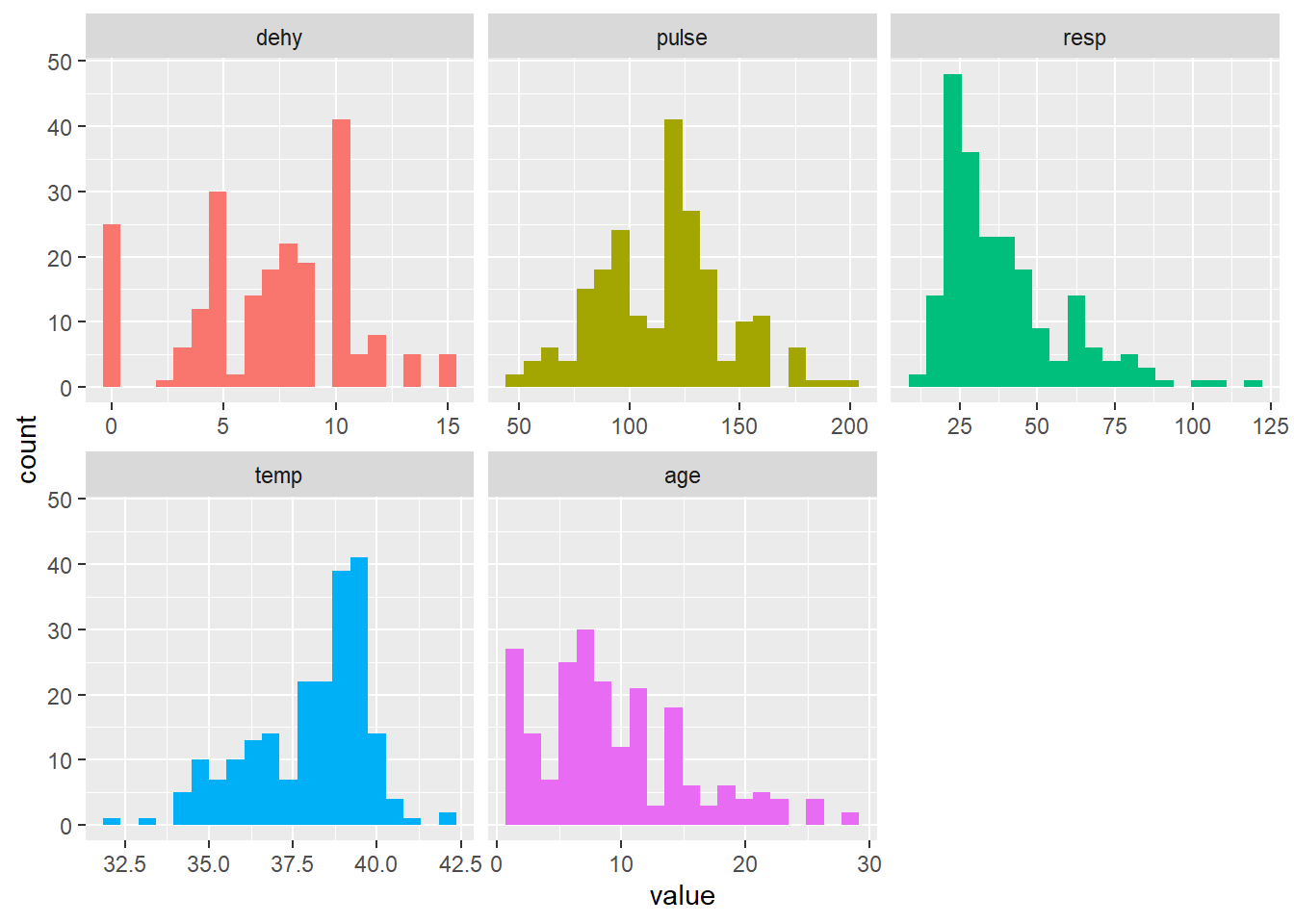
Bref, vous voyez que cela est assez intéressant de rapidement voir toutes vos données numériques…
Avant de passer à l’étape de modéliser on doit réfléchir un peu (ça ne fait jamais de mal…).
Comme pour la régression linéaire dans la mesure où les mathématiques vont nous aider cela vient avec des contraintes…
1 : comme précédemment on veut que notre \(Y\) soit issus d’observations indépendantes (ainsi on ne pourrait pas par exemple évaluer à 2 moments différents les mêmes veaux et faire un modèle ne tenant pas compte que les veaux sont réévalués…)
2 : Pas de colinéarité entre les variables indépendantes (\(x\)’s) Rappelez vous si mes \(x\)’s sont liés entre eux je ne peux pas avoir un modèle stable pour obtenir mes coefficients car je ne peux pas déterminer celui-ci indépendamment de la variable avec laquelle il est corrélé… Cela va augmenter l’instabilité du modèle…
3 : les prédicteurs continus ont une relation linéaire par rapport au \(logit(P(Y=evenement))\) ça c’est plus difficile à montrer car ce n’est pas intuitif au vu de l’échelle à laquelle la relation est linéaire…
Cependant comme le mentionne sur le forum StackExchange Frank Harrell un des maîtres des modèles de régression, il ne faut pas nécessairement tout faire au début pour transformer les données qui ne sont pas normalement distribuées car parfois le pire est l’ennemi du bien. Je vous réfère également à son livre: Regression modeling strategies qui présente le package rms. Ce paquet a développé énormément d’outils en terme de prédiction clinique notamment. Ce qu’il faut retenir est qu’en général la régression logistique est un peu plus permissive que la régression linéaire…
2.2.1 Analyse du modèle glm
Maintenant je vais donc regarder le lien entre la FC et le sepsis en utilisant la fonction glm qui est incluse de base dans R. La seule différence vs lm est que je dois indiquer la famille de glm et le lien.
Ici nous avons une distribution binomiale (puisque le lien linéaire n’est pas en fonction de notre \(Y\) mais de \(f(P(Y=1))\) de notre probabilité d’être en sepsis et le lien entre cette probabilité et le modèle linéaire est un lien logit (voir le paragraphe 2 et les généralités sur la régression logistique).
#ATTENTION TOUT D'ABORD ASSUREZ VOUS QUE VOUS PRÉDISEZ BIEN CE QUE VOUS VOULEZ PRÉDIRE AVEC LE BON RÉFÉRENT...
levels(factor(veaux$sepsis)) # mon référent est "0" je prédis sepsis=1 (c'était déjà le cas puisque R par défaut classe soit pas ordre numérique croissant ou par ordre alphabétique)## [1] "0" "1"# dans le doute, mettez le clairement une bonne fois pour toute avec "relevel"
#relevel(factor(veaux$sepsis),ref="0") en utilisant cette commande je peux spécifier mon référent...)
#ensuite on réalise notre 1er modèle logistique univarié
l_1 <- glm(sepsis~temp, family = binomial(link = "logit"), data = veaux)
summary(l_1)##
## Call:
## glm(formula = sepsis ~ temp, family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1659 -0.8254 -0.7551 1.4096 1.8488
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.71593 3.24660 1.453 0.1463
## temp -0.14822 0.08559 -1.732 0.0833 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 252.14 on 211 degrees of freedom
## AIC: 256.14
##
## Number of Fisher Scoring iterations: 4OK donc vous voyez que c’est très similaire à ce que nous avons vu pour les modèles linéaires comme type d’output et c’est normal puisque c’est juste une autre version de modèle linéaire. Sur l’échelle logit chaque augmentation d’un degré de température diminue le \(logit(P(sepsis)\) de -0.16697). Vous voyez également que nous avons certains indices qui sont indiqués sur l’output tel que le critère d’information d’Akaike (AIC). Ce critère avec d’autres également, peut être utilisé pour évaluer différents modèles en compétition avec d’autres indices selon le principe lower is better. Une valeur plus basse est meilleure. La déviance est aussi un de ces indicateurs. Dans la sortie du modèle on a 2 déviances.
- La déviance nulle qui correspond à la déviance du modèle nul avec uniquement l’intercept.
- La déviance résiduelle est la déviance du modèle complet.
si je veux traduire le résultat de mon modèle de façon plus directe
Je dois aller sur l’échelle originale de mon \(y\) puisque la sortie de mon modèle est sur l’echelle \(logit(p)\):
exp(coefficients(l_1))## (Intercept) temp
## 111.7131778 0.8622404Ici je me suis servi de la fonction exp de R pour exponentier mon coefficient (en fait tous les coefficients de l’objet glm).
Donc le rapport de cote de la probabilité de sepsis et de 0.846 pour chaque degré de différence de température. Je pourrai également le visualiser sous la fonction plot_model de sjTools.
De manière analogue, je peux demander l’intervalle de confiance de ces estimés.
exp(confint(l_1))## 2.5 % 97.5 %
## (Intercept) 0.1860609 67060.817968
## temp 0.7281701 1.020206plot_model(l_1, show.values = TRUE, vline.color = "darkgrey" ) + theme_bw() +ggtitle("") +labs(y="Rapport de cote")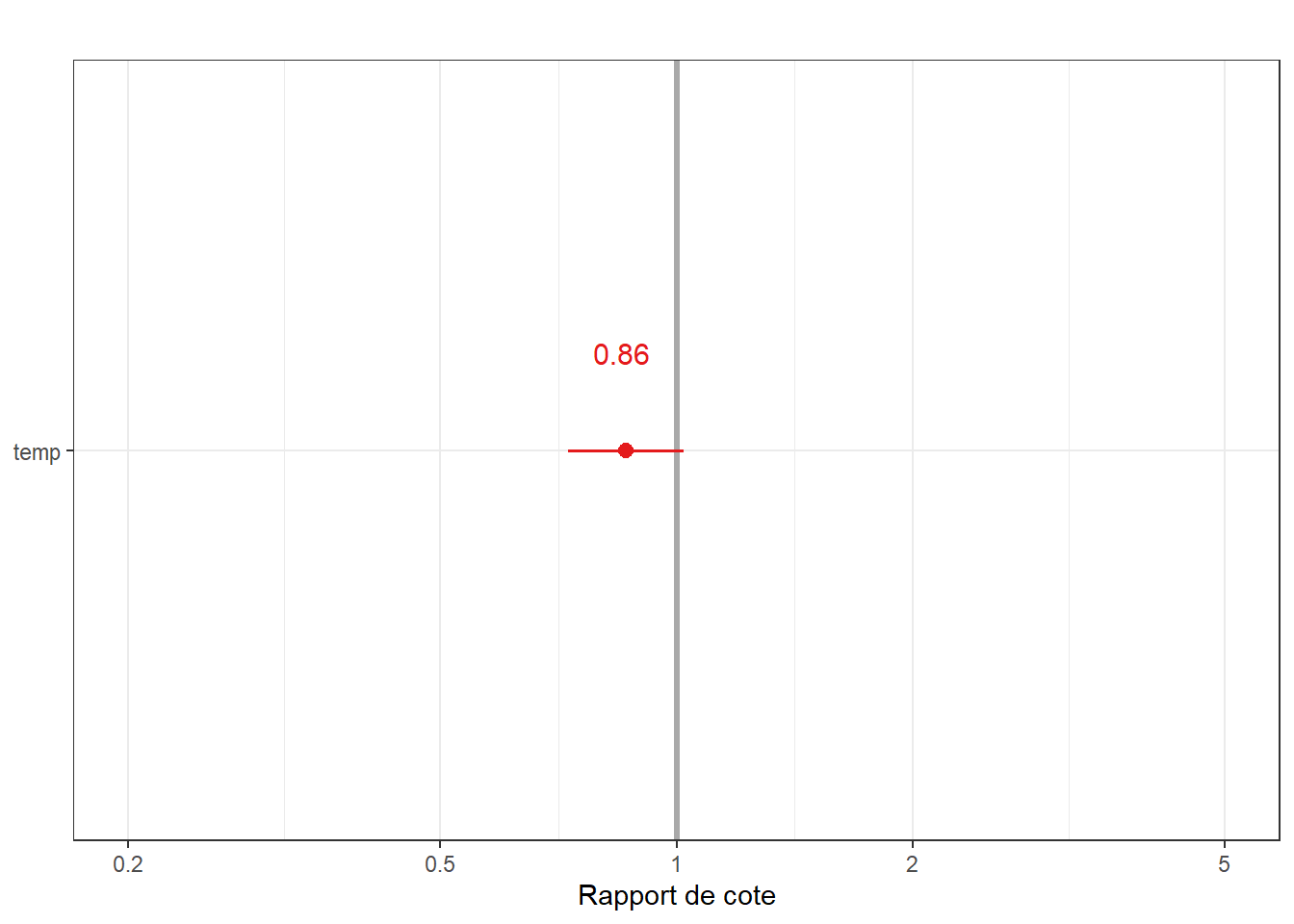
2.2.2 Évaluation du modèle
Comme ce que l’on prédit dans ce modèle est une variable dichotomique, il est impossible d’évaluer les résiduels de la même façon que pour une modèle linéaire.
Comme pour tout modèle je peux regarder l’impact des observations les plus influentes sur mon modèle. Il existe plusieurs façons d’évaluer le modèle en terme d’observations influentes ou outliers. Visuellement la distance de Cook parmi d’autres peut être intéressante. Mon objectif n’est pas de disserter trop longtemps sur ces points car ils dépassent l’objectif du tutoriel et ce sont plus des points à discuter dans un cours. Je vous réfère au cours PTM6685 Epidémiologie 2, ou au livres de Frank Harrell / Ewout Steyerberg décrits précédemment.
#plot(l_1)
plot(l_1, which = 4, id.n = 5) #ici je demande à visualiser les 5 observations avec les plus grandes distances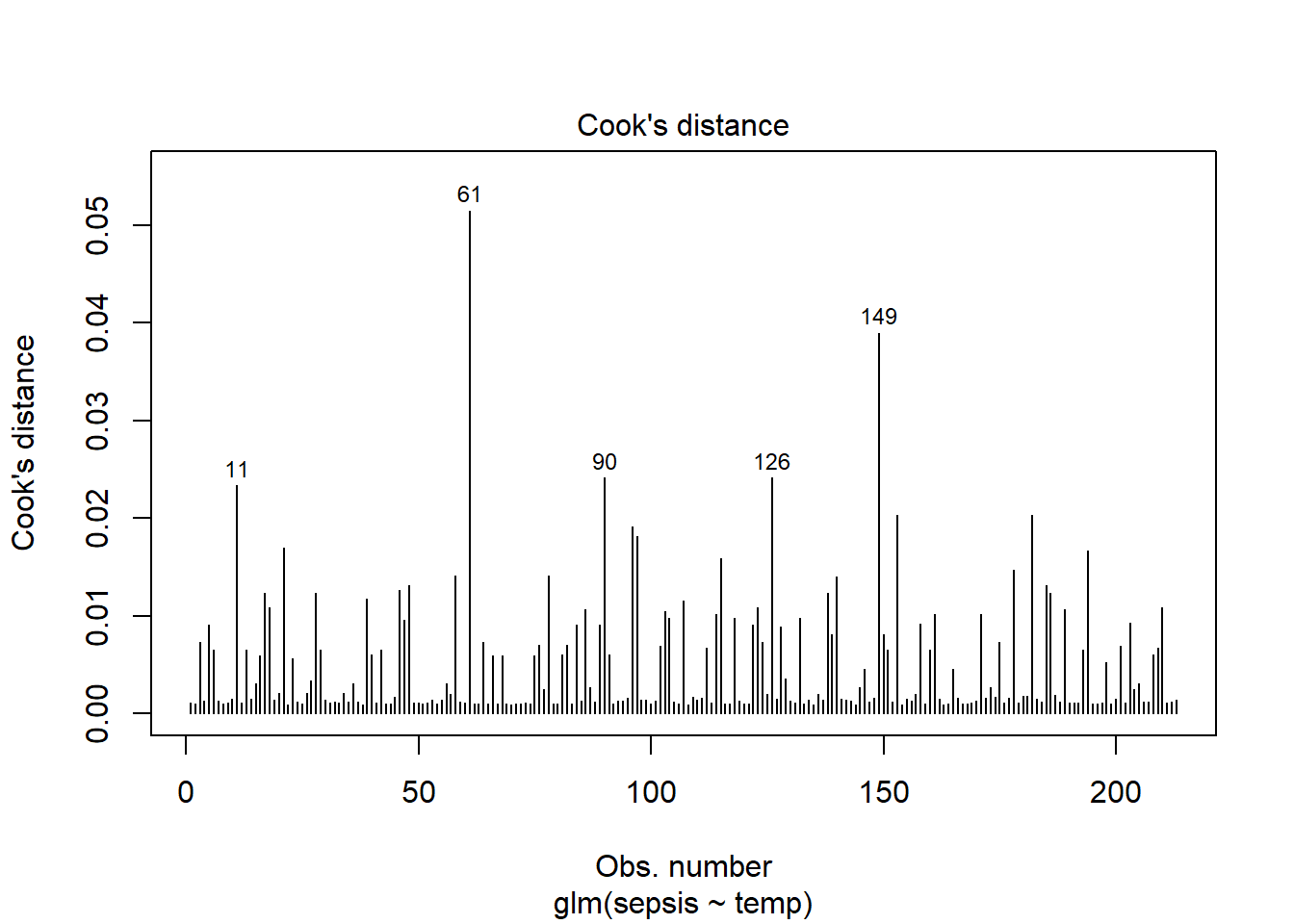
On est un peu moins regardant en terme de résidels sur nos modèles de régression linéaire et c’est un débat qui dépasse un peu là encore ce tutoriel, donc je n’irai pas dans le détail Voir par exemple ce lien.
#ici encore une fois j'utilise la fonction augment() du package broom pour évaluer mes diagnostiques.
model.data <- augment(l_1) %>%
mutate(index = 1:n())
model.data %>% top_n(3, .cooksd)## # A tibble: 4 x 10
## sepsis temp .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
## 1 1 42 -1.51 0.383 1.85 0.0218 1.09 0.0515 1.87 61
## 2 1 34 -0.324 0.366 1.32 0.0327 1.09 0.0241 1.34 90
## 3 1 34 -0.324 0.366 1.32 0.0327 1.09 0.0241 1.34 126
## 4 0 32 -0.0271 0.527 -1.17 0.0694 1.09 0.0390 -1.21 149ggplot(model.data, aes(index, .std.resid)) +
geom_point(aes(color = factor(sepsis)), alpha = .5) +
theme_bw()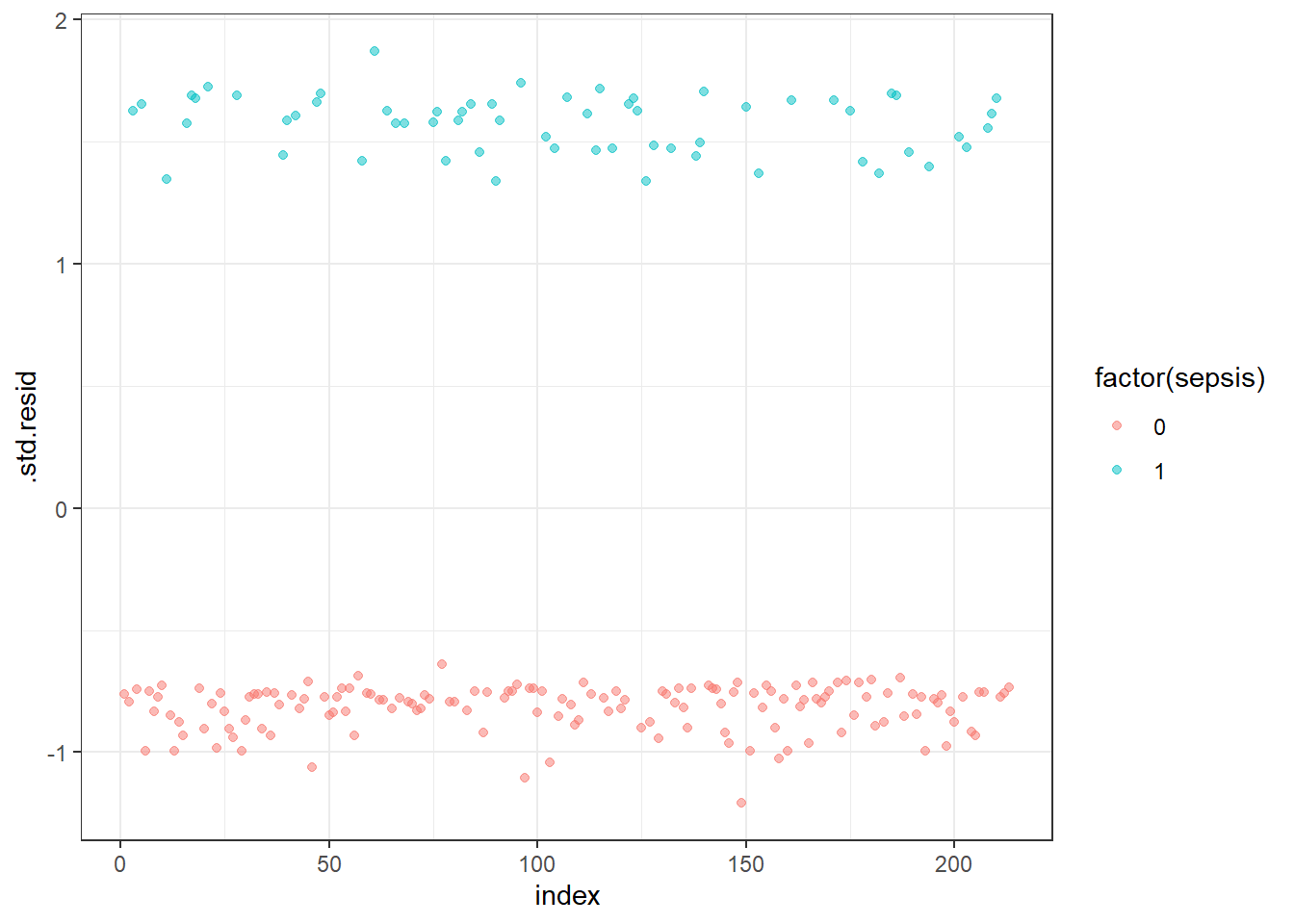
Je demande ensuite les résiduels standardisés qui dépassent 3 (normalement il ne devrait pas y en avoir dans un monde idéal…)
model.data %>%
filter(abs(.std.resid) > 3)## # A tibble: 0 x 10
## # ... with 10 variables: sepsis <dbl>, temp <dbl>, .fitted <dbl>,
## # .se.fit <dbl>, .resid <dbl>, .hat <dbl>, .sigma <dbl>, .cooksd <dbl>,
## # .std.resid <dbl>, index <int>Ici cela fonctionne. Si jamais cela ne fonctionnait pas je devrais regarder les données qui ont un impact afin notamment de décider de la meilleure conduite à tenir (éliminer ces données si c’est justifié (ex erreur de saisie), transformer la variable continue par exemple…) => ceci dépasse le cadre du tutoriel…
ATTENTION: ELIMINER DES DONNÉES JUSTE PARCE QUE CE SONT DES OUTLIERS N’EST PAS UNE BONNE PRATIQUE… LA VIE EST IMPARFAITE ET LES MODÈLES AUSSI. SI ON ÉLIMINE CE QUI NE NOUS PLAIT PAS ON SURESTIME LA PERFORMANCE DU MODÈLE… (ET ON NE FAIT PAS DE LA BONNE SCIENCE…) => voir cette page sur la gestion des outliers
2.3 Relation entre la variable dépendente et des variables catégoriques
Maintenant on peut par exemple voir si la probabilité de sepsis est liée à l’âge que je vais catégoriser (désolé pour les puristes car effectivement la catégorisation est rarement une bonne idée quand on a une variable continue mais c’est à des fins d’illustration : Que les puristes me pardonnent!!!)
#je vais catégoriser l'age en quintiles...
#d'abord juste pour que vous les voyiez:
quantile(veaux$age, c(0, 0.2, 0.4, 0.6, 0.8, 1), na.rm=TRUE)## 0% 20% 40% 60% 80% 100%
## 1 4 7 10 14 28#ensuite j'utilise simplement dplyr et la fonction ntile
veaux <- veaux %>% mutate(age_c = ntile(age, 5))
veaux %>% freq(age_c)## Frequencies
## veaux$age_c
##
## Freq % Valid % Valid Cum. % Total % Total Cum.
## ----------- ------ --------- -------------- --------- --------------
## 1 43 20.19 20.19 20.19 20.19
## 2 43 20.19 40.38 20.19 40.38
## 3 43 20.19 60.56 20.19 60.56
## 4 42 19.72 80.28 19.72 80.28
## 5 42 19.72 100.00 19.72 100.00
## <NA> 0 0.00 100.00
## Total 213 100.00 100.00 100.00 100.00Je vous disais qu’on peut être intéressé à voir la distribution de notre prédicteur catégorique en fonction de l’évènement à prédire.
pour cela je vous présente la fonction cross_plot de funModeling.
Notez:
- 1 je spécifie mon \(x\) (input)
- 2 je spécifie ma variable dépendente (\(y\) qui est la cible de ma prédiction (argument target))
- 3 par défaut j’ai mes données qui sont ramenées à 100% ainsi que les valeurs réelles observées
cross_plot(veaux, input = "age_c", target = "sepsis")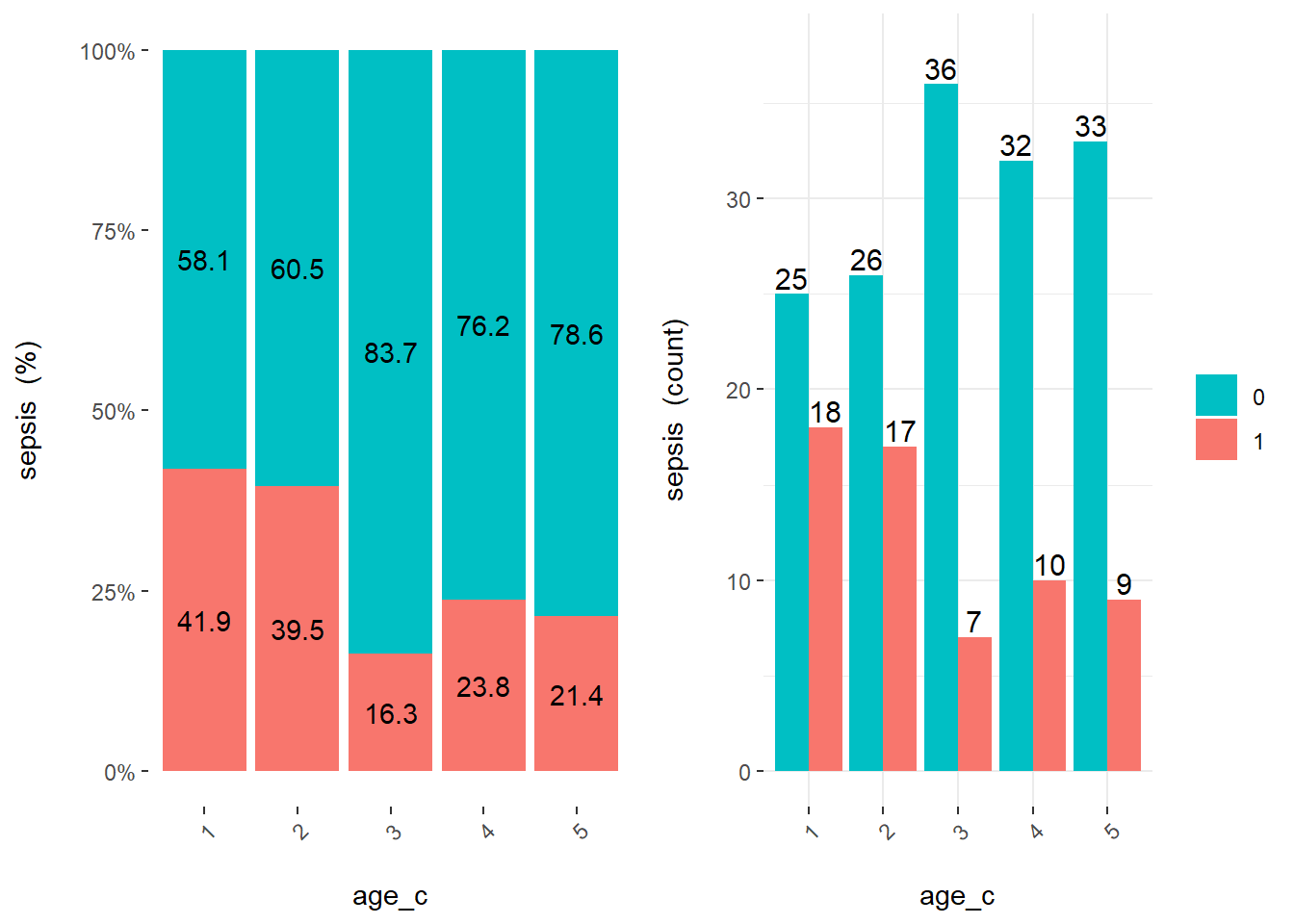
cross_plot(veaux, input = "age_c", target = "sepsis", plot_type = "percentual") # je peux sélectionner un des 2 panneaux...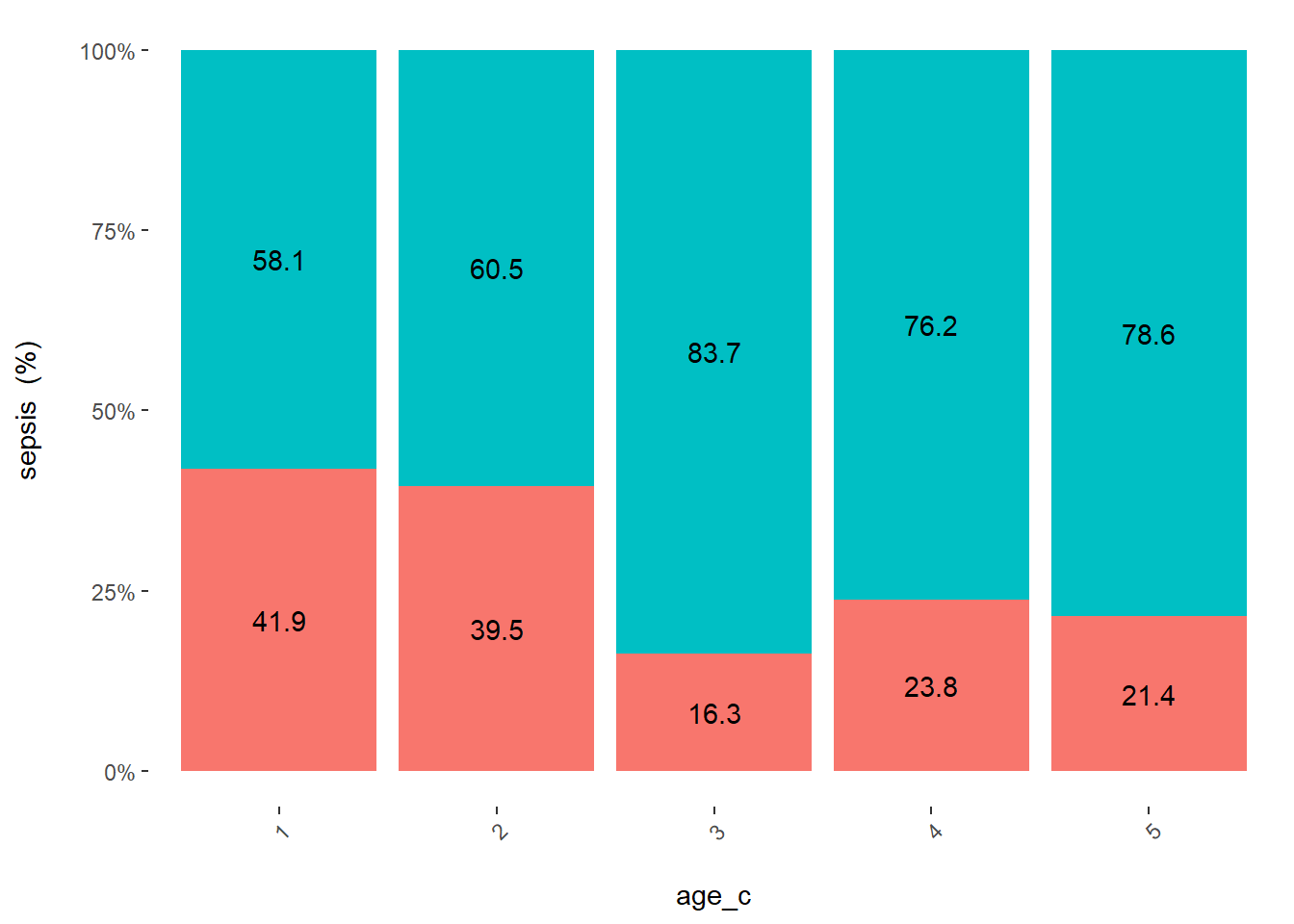
On voit qu’il se passe quelque chose entre les catégories 1 et 2 vs 3, 4, 5 (on sait tous que la septicémie est plus probable chez les jeunes veaux…).
l_2 <- glm(sepsis~age_c, family = binomial(link = "logit"), data=veaux)
summary(l_2)##
## Call:
## glm(formula = sepsis ~ age_c, family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.0205 -0.8081 -0.7140 1.3429 1.8544
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.09565 0.34276 -0.279 0.7802
## age_c -0.28528 0.11150 -2.558 0.0105 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 248.33 on 211 degrees of freedom
## AIC: 252.33
##
## Number of Fisher Scoring iterations: 4Ici il y un problème. Souvenez vous ce que nous avons vu précédemment. Si j’ai \(n\) catégories je devrais avoir \((n-1)\) coefficients.
str(veaux$age_c)## int [1:213] 1 1 1 3 1 4 1 3 2 2 ...C’est bien que que nous pensions. R a d’emblée pensé que c’était un chiffre (integer format). On doit donc le préciser dans notre régression.
l_2b <- glm(sepsis~factor(age_c), family = binomial(link = "logit"), data=veaux)
summary(l_2b)##
## Call:
## glm(formula = sepsis ~ factor(age_c), family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.0415 -0.7375 -0.6945 1.3197 1.9054
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.32850 0.30912 -1.063 0.2879
## factor(age_c)2 -0.09638 0.43914 -0.219 0.8263
## factor(age_c)3 -1.30910 0.51594 -2.537 0.0112 *
## factor(age_c)4 -0.83465 0.47624 -1.753 0.0797 .
## factor(age_c)5 -0.97078 0.48680 -1.994 0.0461 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 244.14 on 208 degrees of freedom
## AIC: 254.14
##
## Number of Fisher Scoring iterations: 4Donc juste pour le visualiser: mise à part le 2ème quintile, on voit que les veaux de le 3ème, 4ème et dernier quintile d’âge on moins de risque de sepsis que les autres.
plot_model(l_2b) #rappelez vous que plot_model est une fonction de sjPlot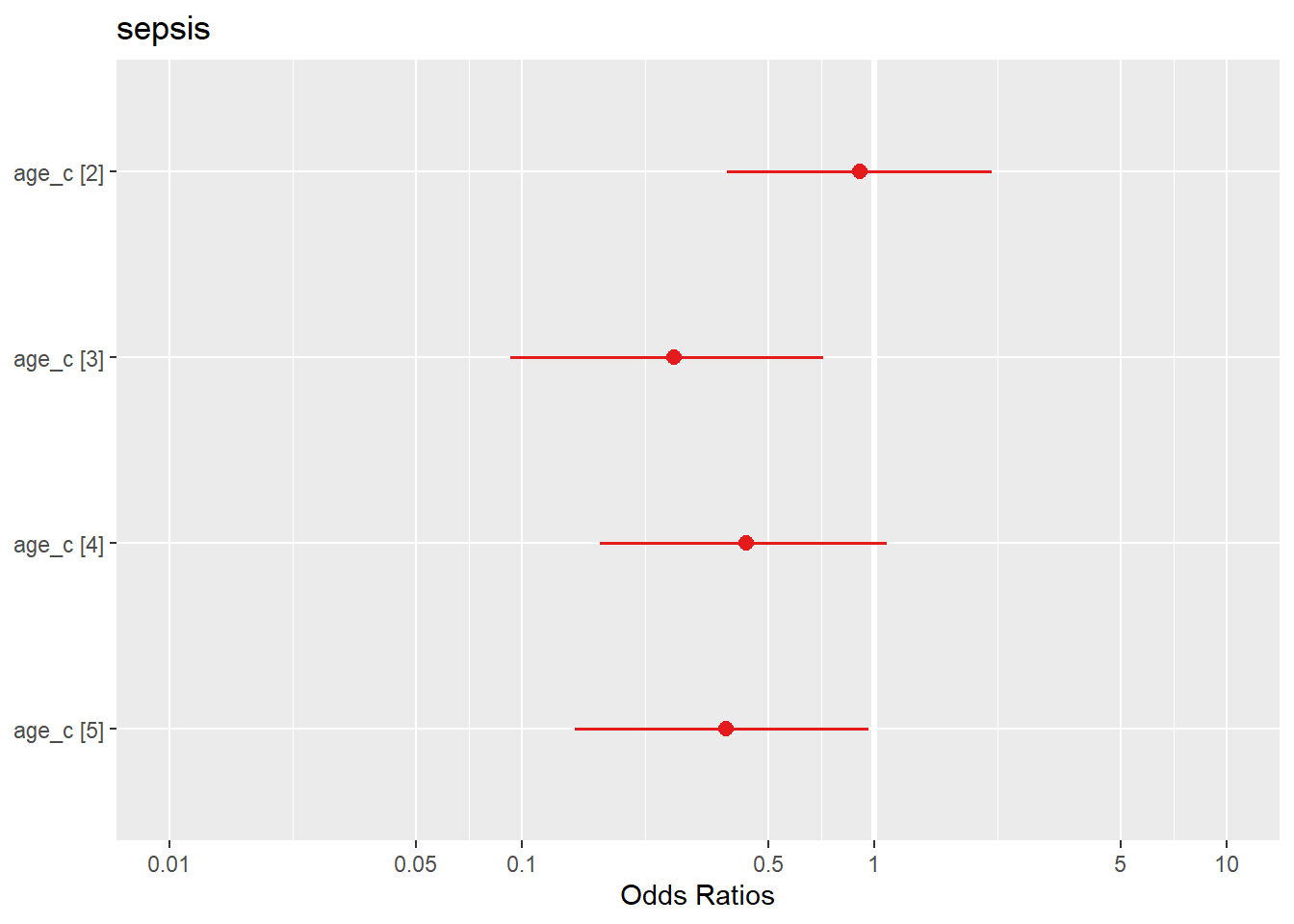
2.4 Régression multivariée
On va maintenant aller à l’étape suivante qui consiste à regarder l’effet de plusieurs covariables en même temps.
veaux$age_c=as.factor(veaux$age_c)
l_mult <- glm(sepsis~age_c+ temp + resp , family = binomial(link = "logit"), data=veaux)
summary(l_mult)##
## Call:
## glm(formula = sepsis ~ age_c + temp + resp, family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5208 -0.8314 -0.5944 1.1418 2.1612
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 8.242027 3.563040 2.313 0.02071 *
## age_c2 0.052883 0.461753 0.115 0.90882
## age_c3 -1.270544 0.543245 -2.339 0.01935 *
## age_c4 -0.706880 0.498171 -1.419 0.15591
## age_c5 -0.844483 0.532157 -1.587 0.11253
## temp -0.246045 0.094349 -2.608 0.00911 **
## resp 0.017119 0.008615 1.987 0.04691 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 235.00 on 206 degrees of freedom
## AIC: 249
##
## Number of Fisher Scoring iterations: 42.5 Diagnostic de fit
Une fois que l’on a notre modèle on doit connaitre ses performances.
On peut créer la matrice de confusion qui nous donne la prédiction de notre modèle vs les observations. Rappelons nous que le modèle prédit une probabilité entre 0 et 1 pour un profil de covariables.
En général on décide que le modèle décide que c’est un cas lorsque P>.5 vs <=.5…
Mais c’est arbitraire.
2.5.1 Aire sous la courbe ROC et discrimination du modèle
Je peux également regarder la courbe ROC de ce modèle et l’aire sous la courbe (ou discrimination) du modèle. Rappel: l’interprétation de l’AUC d’un modèle se fait de la façon suivante. Si je prends au hasard 1 veau avec et 1 veau sans l’issue à prédire alors l’AUC est le pourcentage de chance que mon modèle classe le veau avec sepsis avec une probabilité prédite supérieure au veau sans sepsis
library(pROC)
test_prob = predict(l_mult, newdata = veaux, type = "response")
test_roc = roc(veaux$sepsis ~ test_prob, plot = TRUE, print.auc = TRUE, percent=FALSE, ci=TRUE)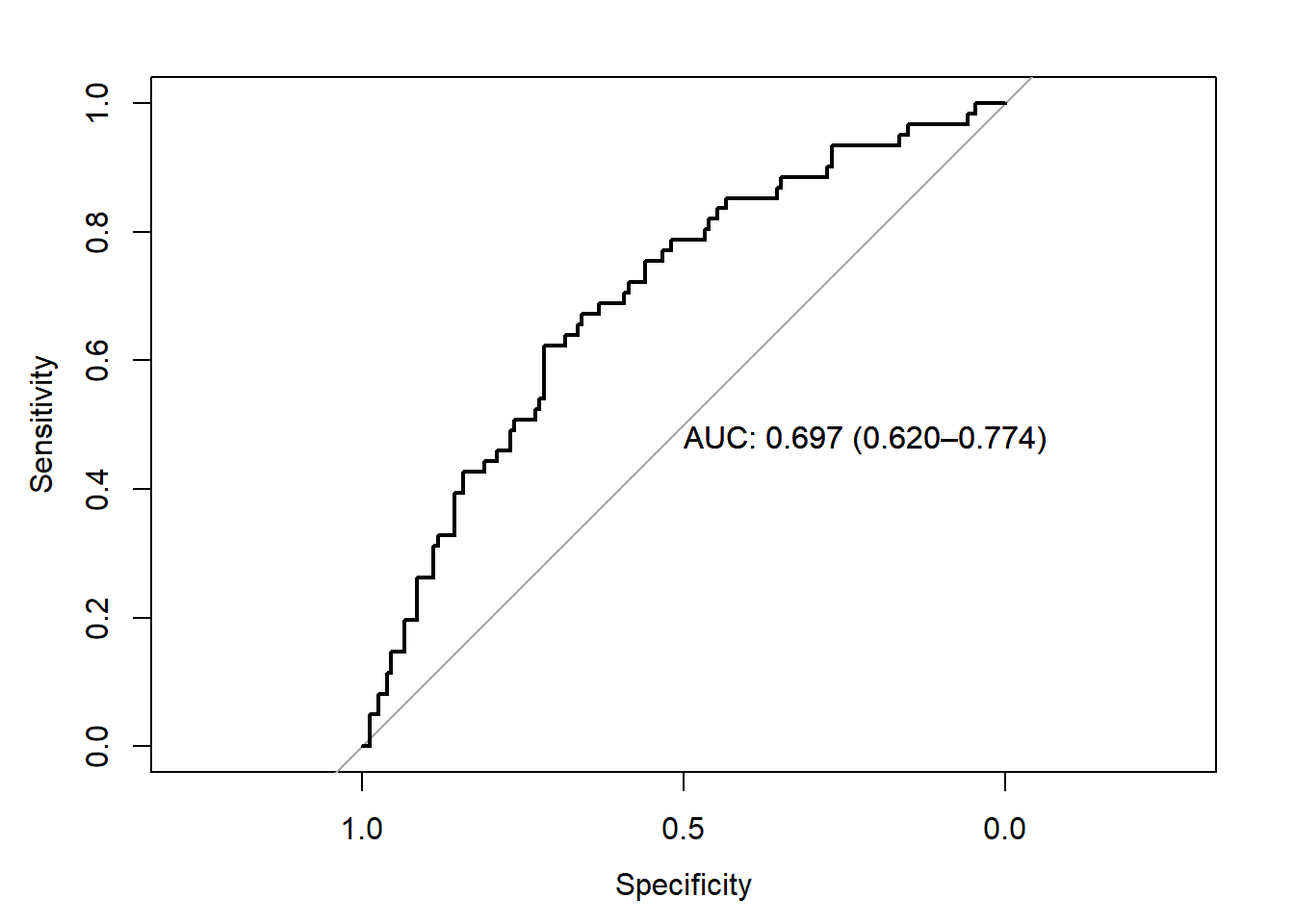
2.5.2 Utilisation du paquet ModelMetrics pour calculer des indice de discrimination/calibration du modèle
Je peux aussi utiliser le paquet ModelMetrics qui me permet d’utiliser directement mon modèle pour tout un tas de diagnostiques tels que l’auc, le score de Brier, coefficient de Gini, ainsi que quelques autres éléments présentés ci-dessous.
- Quelques outils de base
library(ModelMetrics)
auc(l_mult) #aire sous la courbe## [1] 0.6971527brier(l_mult) #score de Brier## [1] 0.1855704gini(l_mult) #coefficient de GINI## [1] 0.3943054- Qualité du modèle
#ici je crée un vecteur avec mes précidictions de mon modèle prediction
prediction <- predict(l_mult, type = 'response')
confusionMatrix(veaux$sepsis, prediction, cutoff=0.5) # me donne la matrice avec en colonne la valeur à prédire (sepsis) et en ligne la prédiction de mon modèle## [,1] [,2]
## [1,] 144 52
## [2,] 8 9Ici j’ai 145 veaux qui ne sont pas en sepsis et qui ont une probabilité de prédiction <.5, j’ai 52 veaux faux négatifs (ie ils sont septiques mais mon modèle leur attribue une probabilité <.5).
J’ai 9 veaux correctement prédits comme septique (j’en manque 52). J’ai 7 veaux non septiques prédits comme septiques…
- Valeurs prédictives positives et négatives du modèle
je peux les calculer directement avec les fonctions ppv et npv
ppv(veaux$sepsis, prediction, cutoff=0.5)## [1] 0.5294118La valeur prédictive positive de mon modèle est de 56% (la confiance que j’ai que c’est un vrai veau en sepsis lorsque mon modèle prédit une probabilité >.5)
npv(veaux$sepsis, prediction, cutoff=0.5)## [1] 0.7346939La valeur prédictive négative de mon modèle est de 74% (la confiance que j’ai que c’est un veau non septique lorsque mon modèle prédit une probabilité <.5)
Notez que pour de nombreuses fonctions vous pouvez adapter le cut-off pour décider de la classification
2.5.3 Autres moyens diagnostiques avec le paquet rms
J’aurai peut être du commencer par là pour ce qui est des diagnostiques d’un modèle de régression logistique. Pourquoi je ne l’ai pas fait, c’est parce que nous avons besoin de respécifier un modèle (le paquet rms ne comprend pas les objets glm)
Je vais utiliser le package rms qui code de façon assez proche que glm mais avec un argument lrm pour logistic regression model.
library(rms)
veaux2=na.omit(veaux)
lrm1 <- lrm(sepsis~age_c + temp + resp, data=veaux2, x=TRUE, y=TRUE) #notez qu'ici vous n'avez pas besoin de préciser le lien puisque lrm est seulement une régression logistique...
lrm1## Logistic Regression Model
##
## lrm(formula = sepsis ~ age_c + temp + resp, data = veaux2, x = TRUE,
## y = TRUE)
##
## Model Likelihood Discrimination Rank Discrim.
## Ratio Test Indexes Indexes
## Obs 213 LR chi2 20.12 R2 0.129 C 0.697
## 0 152 d.f. 6 g 0.826 Dxy 0.394
## 1 61 Pr(> chi2) 0.0026 gr 2.285 gamma 0.394
## max |deriv| 2e-07 gp 0.157 tau-a 0.162
## Brier 0.186
##
## Coef S.E. Wald Z Pr(>|Z|)
## Intercept 8.2420 3.5630 2.31 0.0207
## age_c=2 0.0529 0.4618 0.11 0.9088
## age_c=3 -1.2705 0.5432 -2.34 0.0193
## age_c=4 -0.7069 0.4982 -1.42 0.1559
## age_c=5 -0.8445 0.5322 -1.59 0.1125
## temp -0.2460 0.0943 -2.61 0.0091
## resp 0.0171 0.0086 1.99 0.0469
## D’emblée vous avez ici plus d’indices concernant le fit du model… Vous retrouvez l’aire sous la courbe (c) ainsi que différents autres indices…
Ce paquet permet aussi de réaliser des nomogrammes qui peuvent aussi être intéressant pour présenter à des praticiens afin de voir concrêtement comment utiliser votre modèle (par exemple sans aller dans le détail…)
#je dois créer mon nomogramme
ddist <- datadist(veaux) #cela permet de créer un résumé de ma BD qui va être utilisé plus tard...
options(datadist='ddist')
nomo <- nomogram(lrm1,
lp.at=seq(-3,4,by=0.5),
fun=function(x)1/(1+exp(-x)),
fun.at=c(.001,.01,.05,seq(.1,.9,by=.1),.95,.99,.999),
funlabel="Risque de sepsis",
#conf.int=c(0.1,0.7), #intervalles de confiance à spécifier
abbrev=FALSE,
minlength=1,lp=F)
plot(nomo)
#juste pour vous montrer des possibilités...On pourrait notamment se servir de différentes fonctions de ce type pour créer une application web qui permet à un vétérinaire de se servir de votre modèle de prédiction (voir d’actualiser vos données selon ses propres observations). Mais ceci est définitivement une autre histoire…
JE N’IRAI PAS PLUS LOIN AVEC TOUTES LES POSSIBILITÉS DE DÉTERMINATION DE LA JUSTESSE DE NOTRE PRÉDICTION ET DE LA VISUALISATION DES PRÉDICTIONS
JE PENSE QUE VOUS VOYEZ LE POTENTIEL…
2.6 Comparaison de plusieurs modèles possibles ou alternatifs
Ici je mets des modèles compétiteurs uniquement à titre d’exemple. Encore une fois, je veux être visuel donc mon argumentaire ne se basera pas sur des analyses de fit traditionnels mathématiques (qui devront être envisagés lorsque vous évaluez et choisissez un modèle vs un autre en vue de publication).
Mon but est encore une fois de vous montrer la façon de visualiser les modèles les uns par rapport aux autres.
l_mult_2 <- glm(sepsis~age_c + resp + pulse, family = binomial(link = "logit"), data=veaux)
summary(l_mult_2)##
## Call:
## glm(formula = sepsis ~ age_c + resp + pulse, family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4191 -0.8441 -0.6480 1.2525 2.0464
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.178611 0.826221 -0.216 0.829
## age_c2 0.068323 0.456869 0.150 0.881
## age_c3 -1.156498 0.532891 -2.170 0.030 *
## age_c4 -0.726864 0.494668 -1.469 0.142
## age_c5 -0.820103 0.527197 -1.556 0.120
## resp 0.013566 0.008367 1.621 0.105
## pulse -0.006901 0.005593 -1.234 0.217
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 240.40 on 206 degrees of freedom
## AIC: 254.4
##
## Number of Fisher Scoring iterations: 4l_mult_3 <- glm(sepsis~age_c + temp + factor(umb), family = binomial(link = "logit"), data=veaux)
summary(l_mult_3)##
## Call:
## glm(formula = sepsis ~ age_c + temp + factor(umb), family = binomial(link = "logit"),
## data = veaux)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5794 -0.8407 -0.5761 1.0580 2.3436
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 8.66116 3.61034 2.399 0.01644 *
## age_c2 -0.16420 0.45480 -0.361 0.71807
## age_c3 -1.57683 0.54224 -2.908 0.00364 **
## age_c4 -0.92171 0.49124 -1.876 0.06062 .
## age_c5 -1.24019 0.52302 -2.371 0.01773 *
## temp -0.24050 0.09403 -2.558 0.01054 *
## factor(umb)1 1.02563 0.36416 2.816 0.00486 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 255.12 on 212 degrees of freedom
## Residual deviance: 231.06 on 206 degrees of freedom
## AIC: 245.06
##
## Number of Fisher Scoring iterations: 4Maintenant par exemple on peut comme précédemment comparer des modèles :
sjPlot::plot_models(l_mult, l_mult_2, l_mult_3, vline.color = "darkgrey") + theme_bw()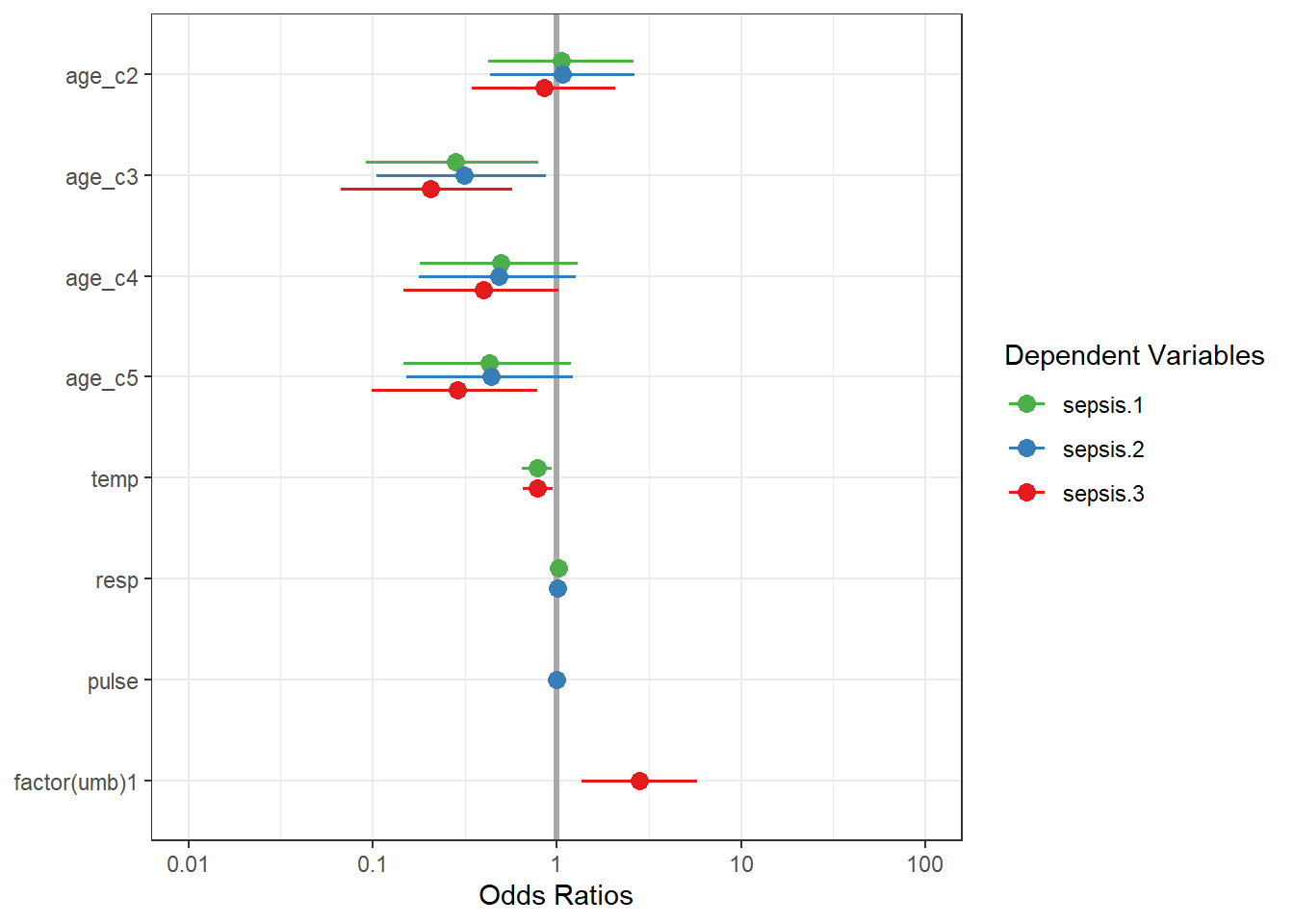
Bon vous comprenez le principe!!!
3. Conclusions
Mon objectif était une simple initiation à R et à ses nombreuses possibilités. Comme vous l’avez vu, on peut très rapidement réaliser des analyses. Cependant rappelez vous toujours qu’il est important de les planifier à l’avance (on peut rapidement se perdre si nos questions ne sont pas clairement établies et pré-définies). Rappelez vous aussi qu’il est crucial de bien consigner sur votre script les commentaires ou décisions que vous prenez afin d’expliciter le code au maximum. Le but est de pouvoir y retourner si il y a un problème ou un ajustement à faire.

1.2.3.2 Comment comparer 2 niveaux lorsqu’aucun n’est un référent?
a. Méthode pour redéfinir le référent
Mais comment faire si je voulais savoir la différence entre la catégorie 2 et 3? Plusieurs techniques sont possibles parmi lesquelles la technique de redéfinir simplement la variable de référence (en utilisant la fonction
relevelque nous avons déjà vu précédemment).#je spécifie que le niveau 2 est ma catégorie de référence beef1$classif=relevel(beef1$classif, "2") m_2r <- lm(data=beef1, carc_wt~classif) summary(m_2r)## ## Call: ## lm(formula = carc_wt ~ classif, data = beef1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -98.495 -29.859 -1.868 29.459 147.414 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 327.132 2.536 128.985 < 2e-16 *** ## classif1 17.464 4.159 4.199 3.19e-05 *** ## classif3 -25.768 6.721 -3.834 0.000143 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 42.21 on 484 degrees of freedom ## Multiple R-squared: 0.07979, Adjusted R-squared: 0.07599 ## F-statistic: 20.98 on 2 and 484 DF, p-value: 1.823e-09Donc ici je vois que la classification 3 entraine une diminution de 25.8kg vs la classif 2… qui est mon référent.
b. Méthode plus généralisable à de nombreux cas…
On peut aussi demander à directement comparer toutes les strates avec le paquet
multcompqui va utiliser notre modèle m_2 pour comparer les niveaux de notre variableclassifqui sont1, 2, 3.library(multcomp) summary(glht(m_2, mcp(classif="Tukey")))## ## Simultaneous Tests for General Linear Hypotheses ## ## Multiple Comparisons of Means: Tukey Contrasts ## ## ## Fit: lm(formula = carc_wt ~ classif, data = beef1) ## ## Linear Hypotheses: ## Estimate Std. Error t value Pr(>|t|) ## 2 - 1 == 0 -17.464 4.159 -4.199 < 1e-04 *** ## 3 - 1 == 0 -43.232 7.043 -6.139 < 1e-04 *** ## 3 - 2 == 0 -25.768 6.721 -3.834 0.000327 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## (Adjusted p values reported -- single-step method)Ici je vois que la carcasse 3 est 25.768kg de moins lourde que la carcasse 2… (3-2 <0).
Notez que la valeur de P est plus importante ici car on a ajusté pour des comparaisons multiple (augmentation de l’erreur de type 1 (alpha)).
ATTENTION
Toujours important d’ajuster pour le nombre de comparisons ;-)